题目内容
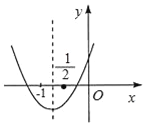
【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c﹣b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】由图象可知,a>0,b>0,c>0,
∵﹣![]()
![]() >﹣1,
>﹣1,
∴b<2a,故①正确,
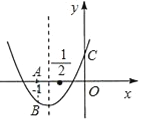
如图易知A(﹣1,0),B(﹣1,a﹣b+c),C(0,c),
当AB=OC时,﹣(a﹣b+c)=c,可得a+2c﹣b=0,
当AB>OC时,﹣(a﹣b+c)>c,可得a+2c﹣b<0,
当AB<OC时,﹣(a﹣b+c)<c,可得a+2c﹣b>0,
故②错误,
∵﹣![]()
![]() <﹣
<﹣![]()
![]() ,
,
∴b>a,
设x1>x2
∵﹣![]()
![]() <x1<0,﹣2<x2<﹣1,
<x1<0,﹣2<x2<﹣1,
∴x1x2<1,
∴![]()
![]() <1,
<1,
∴a>c,
∴b>a>c,故③正确,
∵b2﹣4ac>0,
∴2ac<![]()
![]() b2,
b2,
∵b<2a,
∴![]()
![]() <3ab,
<3ab,
∴![]()
![]() b2=b2+
b2=b2+![]()
![]() b2>b2+2ac,
b2>b2+2ac,
b2+2ac<![]()
![]() b2<3ab,
b2<3ab,
故选C.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】小明根据学习函数的经验,对函数![]() 的图像与性质进行了探究.请补充完整:
的图像与性质进行了探究.请补充完整:
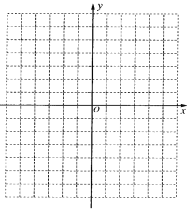
(1)先填表,再在如图所示的平面直角坐标系中,描全表中各对对应值为坐标的点,并画出该函数的图像:
x | … | -5 | -4 | -3 | -2 | 0 | 1 | 2 | 3 | … |
| … | 2 |
| 3 | -3 |
| 0 | … |
(2)结合函数的图像,说出两条不同类型的性质;
①________________________________;____________________________________.
②![]() 的图像是由
的图像是由![]() 的图像如何平移得到?
的图像如何平移得到?
___________________________________________.
(3)当函数值![]() 时,x的取值范围是____________span>.
时,x的取值范围是____________span>.