题目内容
【题目】如图，矩形
中，
，
，过对角线
中点
的直线分别交
、
于点
，
．
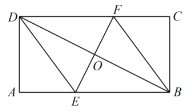
（1）求证：四边形
是平行四边形；
（2）当四边形是菱形时，求菱形的面积．
【答案】（1）见解析；（2）20.
【解析】
（1）根据平行四边形ABCD的性质，判定△BOE≌△DOF（ASA），得出四边形BEDF的对角线互相平分，进而得出结论；
（2）在Rt△ADE中，由勾股定理得出方程，解方程求出BE，根据平行四边形的面积公式即可得到结论．
（1）证明：∵四边形ABCD是矩形，O是BD的中点，
∴∠A=90°，AD=BC=4，AB∥DC，OB=OD，
∴∠OBE=∠ODF，
在△BOE和△DOF中，
，
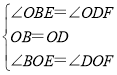∴△BOE≌△DOF（ASA），
∴EO=FO，
∴四边形BEDF是平行四边形；
（2）解：当四边形BEDF是菱形时，
设BE=x，则DE=x，AE=8-x．
在Rt△ADE中，DE2=AD2+AE2，
在
中，
，
，
解得：
，即BE=5，
.
【题目】某单位宿舍用电规定如下：如果每户一个月的用电量不超过
度，那么这个月只需要交10元电费，若超过度，则这个月除了要交10元电费外，超过的部分还要按
元交费，下表是某户5月份和6月份的用电和交费情况，求的值.
月份 | 用电量（度） | 交电费总数（元） |
5 | 80 | 25 |
6 | 45 | 10 |
【题目】暑假到了，即将迎来手机市场的销售旺季．某商场销售甲、乙两种品牌的智能手机，这两种手机的进价和售价如下表所示：
甲 | 乙 | |
进价（元/部） | 4000 | 2500 |
售价（元/部） | 4300 | 3000 |
该商场计划投入15.5万元资金，全部用于购进两种手机若干部，期望全部销售后可获毛利润不低于2万元．（毛利润=（售价﹣进价）×销售量）
（1）若商场要想尽可能多的购进甲种手机，应该安排怎样的进货方案购进甲乙两种手机？
（2）通过市场调研，该商场决定在甲种手机购进最多的方案上，减少甲种手机的购进数量，增加乙种手机的购进数量．已知乙种手机增加的数量是甲种手机减少的数量的2倍，而且用于购进这两种手机的总资金不超过16万元，该商场怎样进货，使全部销售后获得的毛利润最大？并求出最大毛利润．
