题目内容
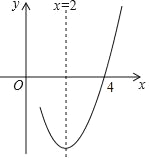
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②4a+b+c=0;③a﹣b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.其中结论正确的是( )
A.①②③B.①②④C.①④⑤D.③④⑤
【答案】B
【解析】
根据题意和二次函数的性质可以判断各个小题是否成立,从而可以解答本题.
①∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),∴抛物线与x轴的另一交点坐标为(0,0),结论①正确;
②∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线过原点,∴﹣![]() =2,c=0,∴b=﹣4a,c=0,∴4a+b+c=0,结论②正确;
=2,c=0,∴b=﹣4a,c=0,∴4a+b+c=0,结论②正确;
③∵当x=﹣1和x=5时,y值相同,且均为正,∴a﹣b+c>0,结论③错误;
④当x=2时,y=ax2+bx+c=4a+2b+c=(4a+b+c)+b=b,∴抛物线的顶点坐标为(2,b),结论④正确;
⑤观察函数图象可知:当x<2时,y随x增大而减小,结论⑤错误.
综上所述:正确的结论有:①②④.
故选B.

练习册系列答案
相关题目