��Ŀ����
����Ŀ����ͼ1����������ȫ��ͬ��������ֽƬABC��DEC�غϷ��ã�����![]() ��
��![]() .
.
��1����������
�ٹ̶�![]() ��ʹ
��ʹ![]() �Ƶ�C��ת.����Dǡ������AB����ʱ����ͼ2�����߶�DE��AC��λ�ù�ϵ��________����֤����
�Ƶ�C��ת.����Dǡ������AB����ʱ����ͼ2�����߶�DE��AC��λ�ù�ϵ��________����֤����
����![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ��������ϵ��________.
��������ϵ��________.
��2��������֤
��![]() �Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����
�Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����![]() ��
��![]() ��������ϵ��Ȼ����������ֱ�����
��������ϵ��Ȼ����������ֱ�����![]() ��
��![]() ��BC��CE���ϵĸߣ����ɴ�֤��С���IJ���.
��BC��CE���ϵĸߣ����ɴ�֤��С���IJ���.
��3����չ̽��
��֪![]() ����D�����ƽ������һ�㣬
����D�����ƽ������һ�㣬![]() ��
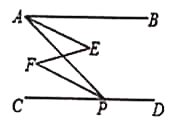
��![]() ��BC�ڵ�E����ͼ4��������������BA���Ƿ���ڵ�F��ʹ
��BC�ڵ�E����ͼ4��������������BA���Ƿ���ڵ�F��ʹ![]() �������ڣ���ֱ��д�����������ĵ�F�ĸ������������ڣ���˵������.
�������ڣ���ֱ��д�����������ĵ�F�ĸ������������ڣ���˵������.
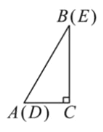
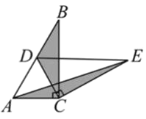
ͼ1 ͼ2
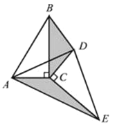
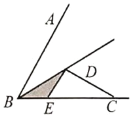
ͼ3 ͼ4
���𰸡���1��![]() ���ɼ�������
���ɼ�������![]() ����2������������3����������.
����2������������3����������.
��������
��1����������ת�����ʿɵ�![]() ��Ȼ�����
��Ȼ�����![]() �ǵȱ������Σ����ݵȱ������ε����ʿɵ�
�ǵȱ������Σ����ݵȱ������ε����ʿɵ�![]() ��Ȼ������ڴ�����ȣ���ֱ��ƽ�н��
��Ȼ������ڴ�����ȣ���ֱ��ƽ�н��
�����ݵȱ������ε����ʿɵ�AC��AD���ٸ���ֱ��������30�������Ե�ֱ�DZߵ���б�ߵ�һ�����AC��![]() AB��Ȼ�����AD��BD���ٸ��ݵȱ������ε����������C��AB�ľ�����ڵ�D��AC�ľ��룬Ȼ����ݵȵȸߵ������ε������Ƚ��
AB��Ȼ�����AD��BD���ٸ��ݵȱ������ε����������C��AB�ľ�����ڵ�D��AC�ľ��룬Ȼ����ݵȵȸߵ������ε������Ƚ��
��2��������ת�����ʿɵ�BC��CE��AC��CD���������ACN����DCM��Ȼ���������ǽDZ���֤����ACN����DCMȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AN��DM��Ȼ�����õȵȸߵ������ε�������֤����
��3������D��![]() ������ı���
������ı���![]() �����Σ��������εĶԱ���ȿɵ�
�����Σ��������εĶԱ���ȿɵ�![]() ��Ȼ����ݵȵȸߵ������ε������ȿ�֪��
��Ȼ����ݵȵȸߵ������ε������ȿ�֪��![]() Ϊ����ĵ㣬����D��
Ϊ����ĵ㣬����D��![]() �����
�����![]() ���Ӷ��õ�
���Ӷ��õ�![]() �ǵȱ������Σ�Ȼ�����
�ǵȱ������Σ�Ȼ�����![]() �������
�������![]() �����á��߽DZߡ�֤��
�����á��߽DZߡ�֤��![]() ȫ�ȣ�����ȫ�������ε������ȿɵõ�
ȫ�ȣ�����ȫ�������ε������ȿɵõ�![]() Ҳ������ĵ㣮
Ҳ������ĵ㣮
��1����![]() ��
��
����֤����������![]() ��������ת��
��������ת��![]() ��
��
����![]() �ǵȱ�������.
�ǵȱ�������.
����![]() ������
������![]() ������
������![]() .
.
�ڡ�AC��![]() AB��AD��AC��
AB��AD��AC��
��AD��BD��
��![]()
��DE��AC��
��![]() ��
��
��![]() .
.
�ʴ�Ϊ��DE��AC��![]() ��
��
��2����ͼ��
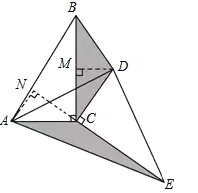
�ߡ�DEC������ABC�Ƶ�C��ת�õ���
��BC��CE��AC��CD��
�ߡ�ACN����BCN��90������DCM����BCN��180��90����90����
���ACN����DCM��
��![]() ��
��![]() ��
�У�
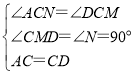 ��
��
��![]() ��AAS����
��AAS����
��AN��DM��
���BDC���������AEC�������ȣ��ȵȸߵ������ε������ȣ���
��![]() ��
��
��3����ͼ������D��![]() ��AB��
��AB��![]() ��
��

��![]() ��
��
���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
�ߡ�ABC��60�㣬BDƽ�֡�ABC��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���ı���![]() �����Σ�
������
��![]() ��
��
��BE��![]() �ϵĸ���ȣ�
�ϵĸ���ȣ�
��![]() ,
,
���![]() ������ĵ㣻
������ĵ㣻
����D��![]() ��
��
��![]() ,
,![]() ��
��
��![]()
��![]() ��
��
��![]() ��
��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��
��BD��CD��
���DBC����DCB��30�㣬
��![]()
��![]() ��
��
![]() ��360��150��60�㣽150�㣬
��360��150��60�㣽150�㣬
��![]() ��
��
����![]() ��
��![]() ��
�У�

��![]() ��SAS����
��SAS����
��![]()
��![]() ,
,
��![]()
���![]() Ҳ������ĵ㣬
Ҳ������ĵ㣬
��������BA�ϴ��ڵ�F�ĸ���������.

 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�