题目内容
【题目】如图，在某月的日历上，圈出
，
，
，
，
，5个数，使它们呈一个十字架.
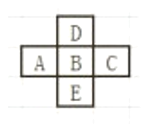
（1）如果它的和为55，求的值；
（2）如果它们的和为115，求D的值;
（3）这五个数的和可以是125吗？
【答案】（1）18；（2）16；（3）不可以，理由见解析
【解析】
（1）由于日历上一个竖列上相邻3个数依次间隔7，可以设竖列上相邻的3个数为x-7，x，x+7，由此得到方程x-7+x+x+7+x-1+x+1=55，解方程根据方程的解即可；
（2）由于日历上一个竖列上相邻3个数依次间隔7，可以设竖列上相邻的3个数为x-7，x，x+7，由此得到方程x-7+x+x+7+x-1+x+1=115，解方程根据方程的解即可；
（3）由于日历上一个竖列上相邻3个数依次间隔7，可以设竖列上相邻的3个数为x-7，x，x+7，由此得到方程x-7+x+x+7+x-1+x+1=125，解方程根据方程的解即可．
(1)设竖列上相邻的3个数为x7，x，x+7，则B=x1，C=x+1，根据题意得出：
x7+x+x+7+x1+x+1=55，
解得：x=11，
故E=x+7=18，
答：E的值为18；
(2)由(1)得出：设竖列上相邻的3个数为x7，x，x+7，则B=x1，C=x+1，根据题意得出：
x7+x+x+7+x1+x+1=115，
解得：x=23，
则D=237=16，
答：D的值为16；
(3)由(1)得出：
设竖列上相邻的3个数为x7，x，x+7，则B=x1，C=x+1，根据题意得出：
x7+x+x+7+x1+x+1=125，
解得x=25，
则x+25=7+25=32，日期不可能大于31，
故不可能五个数的和是125.
练习册系列答案
阅读快车系列答案
相关题目
