��Ŀ����
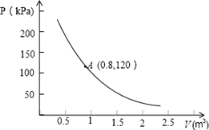
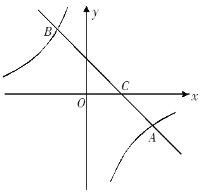
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y =ax+b��ͼ���뷴��������y =![]() ��ͼ����A��4����2����B����2��m�����㣬��x�ύ�ڵ�C.
��ͼ����A��4����2����B����2��m�����㣬��x�ύ�ڵ�C.
��1����a��m��ֵ��
��2����ֱ��д������ʽax+b��![]() �Ľ⼯��
�Ľ⼯��
��3����P�ڷ���������ͼ���ϣ��ҵ�P�ĺ�����Ϊ��4����ƽ��ֱ������ϵ���Ƿ����һ��Q��ʹ����A��B��P��QΪ������ı���Ϊƽ���ı��Σ�������ڣ���ֱ��д����Q������.
���𰸡�(1)a=��1��m=4��(2)x����2��0<x��4��(3)Q1(6��0) ��Q2(2��-4)��Q3 (-10��8).
��������
��1���Ƚ���A������뷴������������ʽ�����k�����������B���꣬���A��B�������ֱ�߽���ʽ�м������a��
��2������ͼ��ֱ�ӵó����ۣ�
��3���������P���꣬�����Q���꣬����ƽ���ı��εĶԽ�����ƽ�ֺ��е����깫ʽ������������⼴�ɵó����ۣ�
��1���ߵ�A��4����2���ڷ���������y��![]() �ϣ�
�ϣ�
��k��4������2������8��
�෴������������ʽΪy����![]() ��
��
�ߵ�B����2����m���ڷ����������ϣ�
�ੁ2m����8��
��m��4��
��B����2��4����
����A��4����2����B����2��4������ֱ��y��ax+b�У���
![]() ��
��
��![]() ��
��
����a����1��m��4��
��2����A��4����2����B����2��4����
���ʽax+b��![]() �Ľ⼯Ϊx����2��0��x��4��
�Ľ⼯Ϊx����2��0��x��4��
��3���ɣ�1��֪�������������Ľ���ʽΪy����![]() ��
��
�ߵ�P�ڷ���������ͼ���ϣ��Һ�����Ϊ��4��
���P��������Ϊ2��
��P����4��2����
���Q��c��n������A��B��P��QΪ������ı���Ϊƽ���ı��Σ�
�ٵ�ABΪ�Խ���ʱ��AB��PQ����ƽ�֣�
��![]() ��4��2����
��4��2����![]() ����4+c����
����4+c����![]() ����2+4����
����2+4����![]() ��2+n����
��2+n����
��c��6��n��0��
��Q��6��0����
�ڵ�APΪ�Խ���ʱ��AP��BQ����ƽ�֣�
��![]() ��4��4����
��4��4����![]() ����2+n����
����2+n����![]() ����2+2����
����2+2����![]() ��4+n����
��4+n����
��c��2��n����4��
��Q��2����4����
�۵�AQΪ�Խ���ʱ��AQ��BP����ƽ�֣�
��![]() ��4+c����
��4+c����![]() ����2��4����
����2��4����![]() ����2+n����
����2+n����![]() ��4+2����
��4+2����
��c����10��n��8��
��Q����10��8����
�������������ĵ�Q������Ϊ��6��0����2����4����10��8����

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�