题目内容
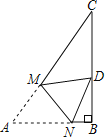
【题目】如图，已知抛物线
经过点
，与
轴交于
两点，
为顶点，
为抛物线上一动点(与点
不重合)
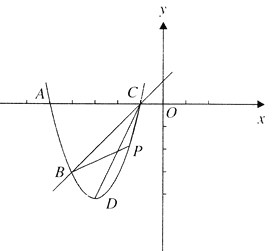
求该抛物线的解析式；
当点在直线
的下方运动时，求
的面积的最大值；
该抛物线上是否存在点，使
？若存在，求出所有点的坐标；若不存在，请说明理由．
【答案】（1）
；（2）
；（3）点
的坐标为
或
【解析】
（1）将点A、B、C坐标代入二次函数表达式，即可求解；
（2）利用S△PBC＝
PG（xCxB），即可求解；
（3）分点P在直线BC下方、上方两种情况，分别求解即可．
解：
抛物线过
两点
可设为
又过点
解析式为；
，
设直线BC的解析式为y=kx+b
把B,C坐标代入得
解得
可得直线
的解析式为：
过点作
轴的垂线，交于点
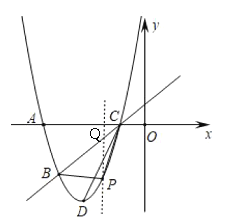
设点的横坐标为
则点的坐标为
，点的坐标为
，
．
当
时，
的面积最大，最大值为；
存在．
∵=
∴顶点
的坐标为
，
连接
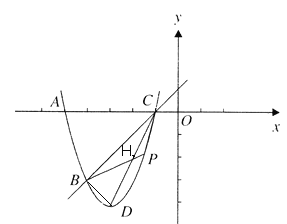
则
是直角三角形，且
．
当点在直线下方时，
设
的中点为
则
，
且点为直线
与抛物线的交点(不与点
重合)
设直线的表达式为y=px+q
把B,H的坐标代入得
解得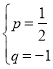
∴直线的表达式为
令
，
解得
(舍去)或
此时的坐标为
当点在直线上方时，
．
设直线CD的解析式为y=mx+n
把C,D的坐标代入得
解得
∴直线的表达式为
，
则可设直线
的表达式为
将点
代入解得
故直线的表达式为
．
令
，
解得或
此时点的坐标为
综上所述，点的坐标为或．
鸿图图书寒假作业假期作业吉林大学出版社系列答案
【题目】甲乙两人依次测量同一圆柱体工件的横截面直径（单位：
），测得的数据分别如表1、表2．
表1：甲的测量数据
测量数据 | 9.8 | 9.9 | 10 | 10.1 | 10.3 |
频数 | 1 | 3 | 3 | 2 | 1 |
表2：乙的测量数据
测量数据 | 9.7 | 9.8 | 10 | 10.1 | 10.3 |
频数 | 1 | 2 | 3 | 2 | 2 |
（1）如果在这些测量数据中选择一个数据作为工件直径的估计值，应该是那个数据？请说明理由.
（2）如果甲再测量一次，求他测量出的数据恰好是估计值的概率；
（3）请直接判断甲乙两人谁的测量技术更好______（填甲或乙），你选择的统计量是_______．
