题目内容
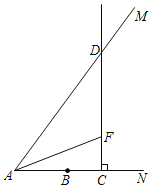
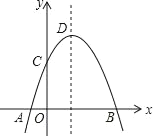
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点(a,0)和点(b,0),交y轴于点C,抛物线顶点为D,下列四个结论中:①当x>0时,y>0;②若a=﹣1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G、F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6![]() .其中正确的有( )个
.其中正确的有( )个
A.0B.1C.2D.3
【答案】C
【解析】
①根据二次函数所过象限,判断出y的符号;
②根据A、B关于对称轴对称,求出b的值;
③根据![]() >1,得到x1<1<x2,从而得到Q点距离对称轴较远,进而判断出y1>y2;
>1,得到x1<1<x2,从而得到Q点距离对称轴较远,进而判断出y1>y2;
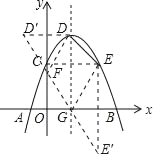
④作D关于y轴的对称点D',E关于x轴的对称点E',连接D'E',D'E'与DE的和即为四边形EDFG周长的最小值.求出D、E、D'、E'的坐标即可解答.
解:①当x>0时,函数图象过一四象限,当0<x<b时,y>0;当x>b时,y<0,故本选项错误;
②二次函数对称轴为x=﹣![]() =1,当a=﹣1时有
=1,当a=﹣1时有![]() =1,解得b=3,故本选项正确;
=1,解得b=3,故本选项正确;
③∵x1+x2>2,
∴![]() >1,
>1,
又∵x1﹣1<1<x2﹣1,
∴Q点距离对称轴较远,
∴y1>y2,故本选项正确;
④如图,作D关于y轴的对称点D′,E关于x轴的对称点E′,
连接D′E′,D′E′与DE的和即为四边形EDFG周长的最小值.
当m=2时,二次函数为y=﹣x2+2x+3,顶点纵坐标为y=﹣1+2+3=4,D为(1,4),
则D′为(﹣1,4);C点坐标为C(0,3);
则E为(2,3),E′为(2,﹣3);
则DE=![]() =
=![]() ;
;
D′E′=![]() =
=![]() ;
;
∴四边形EDFG周长的最小值为![]() +
+![]() ,故本选项错误.
,故本选项错误.
∴正确的有2个.
故选:C.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤50 | a |
C | 51≤m≤75 | 50 |
D | m≥76 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为 ,a= ;
(2)随机抽取一位学生进行调查,刚好抽到A类学生的概率是 ;
(3)若该校有2000名学生,请估计全校学生中家庭藏书不少于76本的人数.