题目内容
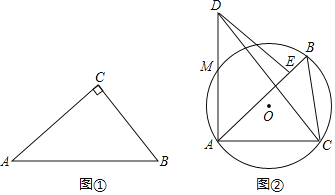
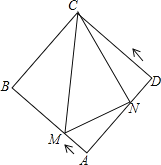
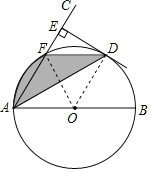
【题目】如图,AB为⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E点.

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=60°,求图中阴影部分的面积.
【答案】(1)见解析;(2)S阴影=![]() π.
π.
【解析】
(1)连接OD,先证明∠OAD=∠CAD,∠ODA=∠CAD,从而证明∠ODE=90°,即可证明DE是⊙O的切线;
(2)连接OF,根据∠BAC=60°和角度转换证明OD∥OC,即可证明S△AFD=S△AFO,把图中阴影部分面积转换得到扇形OAF的面积,再根据扇形面积公式即可求出.
解:(1)连结OD,
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵DE⊥AC,即∠AED=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线;
(2)连接OF,
∵OD∥AC,
∴S△AFD=S△AFO,
∵∠BAC=60°,OA=OF,
∴△OAF为等边三角形,
∴∠AOF=60°,
∴S阴影=S扇形OAF=![]() =
=![]() π.
π.

练习册系列答案
相关题目
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.