题目内容
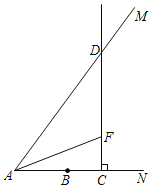
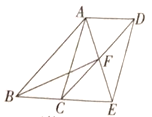
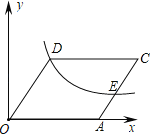
【题目】如图,在平面直角坐标系中,函数y=![]() (x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.
(x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.
【答案】3![]()
【解析】
求出点D或点E的坐标,即可求出k的值,通过作垂线,利用三角形相似,和菱形的性质可以求出点 D 的坐标,进而求出k的值.
过点D、E分别作x轴的垂线,垂足为M、N,
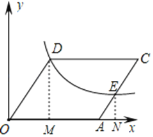
∵ABCD是菱形,
∴OD=AC=OA=8,OD∥AC,
∴∠DOA=∠CAN,
∴△DOM∽△EAN,
∴![]() ,
,
又∵CE=2AE,
∴![]() ,
,
设D(a,b),则OM=a,DM=b,
∴AN=![]() a,EN=
a,EN=![]() b,
b,
∴E(8+![]() a,
a,![]() b)
b)
又∵点D、点E都在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴ab=(8+![]() a)×
a)×![]() b,
b,
解得:a=3,
在Rt△DOM中,b=DM=![]() =
=![]() ,
,
∴k=ab=3![]() ,
,
故答案为:3![]()

练习册系列答案
相关题目
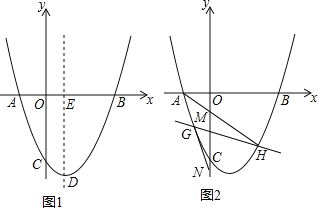
【题目】已知二次函数![]() 的y与x的部分对应值如表:
的y与x的部分对应值如表:
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(![]() ,2),B(
,2),B(![]() ,3)是抛物线上两点,则
,3)是抛物线上两点,则![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5