Question

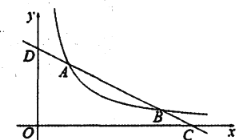
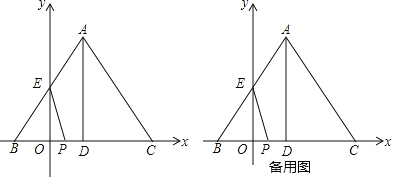
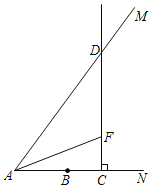
【题目】如图，在△ABC中，点D在△ABC的内部且DB=DC，点E，F在在△ABC的外部，FB=FA，EA=EC，∠FBA=∠DBC=∠ECA.

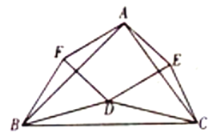
解答下列问题：

（1）①填空：△ACE∽_________∽___________；

②求证：△CDE∽△CBA；

（2）求的值；

（3）若点D在∠BAC的平分线上，判断四边形AFDE的形状，并说明理由.

Answer 1

【答案】（1）①△ABF，△BCD②证明见解析（2）=1（3）四边形AFDE是菱形，理由见解析

【解析】

(1)①根据等腰三角形的性质得到∠DBC=∠DCB，∠FBA=∠FAB，∠ACE=∠EAC,等量代换得到∠FAB=∠BCD=∠EAC,于是得到结论;②根据相似三角形的性质得到，根据相似三角形的判定定理即可得到结论;

(2)根据相似三角形的性质得到∠EDC=∠FBD，∠FDB=∠ACB等量代换得到∠FDB=∠ACB,根据全等三角形的判定即可得到结论;

(3)根据全等三角形的性质得到FB=DE,DF=CE，等量代换得到FD=AE，FA=DE,推出四边形AFDE是平行四边形，连接AD,于是得到AD平分∠BAC,根据菱形的判定定理即可得到结论.

解：（1）①△ABF，△BCD

②∵BD=DC，EA=EC，

∴∠DBC=∠DCB，∠EAC=∠ECA，又∠DBC=∠ECA，

∴∠DBC=∠EAC

∴△ACE∽△BCD，

∴，∠ECD=∠ACB，

∴△CDE∽△CBA

（2）∵△CDE∽△CBA，∠CDE=∠CBA=∠DBF；

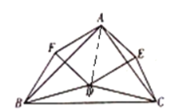
同理，△BFD∽△BAC，

∠FDB=∠ACB=∠ECD，BD=CD，

∴△FBD≌△EDC，

∴FD=EC，=1

（3）AFDE是菱形

∵△FBD≌△EDC，

∴FB=FA=DE，FD=EC=EA

∴AFDE是平行四边形，

∴FA∥DE，连接AD，∠FAD=∠EDA，

又点D在∠BAC的平分线上，∠BAD=∠CAD

∴∠FAD=∠EAD=∠EDA，

∴EA=ED

∴AFDE是菱形