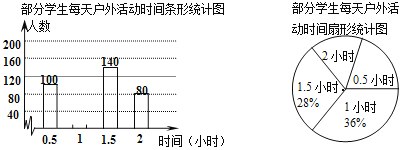
��Ŀ����
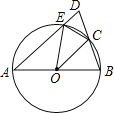
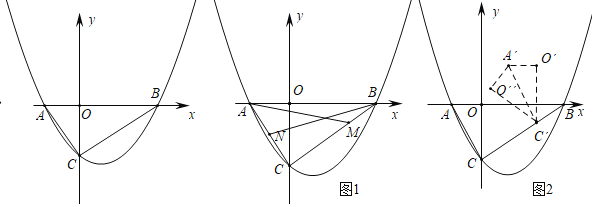
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y��ax2+bx+c��x���ཻ�ڵ�A����1��0����B��3��0������y�ύ�ڵ�C������AC��BC���ҡ�ACB��90����
��1������κ����Ľ���ʽ��
��2����ͼ��1������N��AC���е㣬M��BC��һ�㣬������CM��2BM����AM��BN�ཻ�ڵ�E�����M���������EMB�������
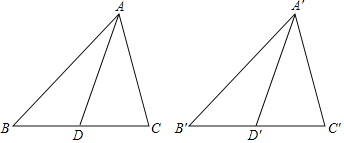
��3����ͼ��2��������AOC��ֱ��BCƽ�Ƶõ���A��O��C�����ٽ���A��O��C����A��C�����۵õ���A��O��C��������AO����AC����������AO��C���ܷɵ��������Σ����ܣ���������з��������ĵ�C�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3��C��������
����3��C��������![]() ����
����![]() ��
��![]() ����
����![]() ����
����
��������
��1����ACB��90�㣬��OC2��OA��OB��3�����C��0����![]() ����������⣻
����������⣻
��2��֤����S��BEM��S��![]() S��ABM��������⣻
S��ABM��������⣻
��3����O��C�䣽AO�塢O��C�䣽AC�䡢AO�壽AC�䣬����������ֱ���⼴�ɣ�
�⣺��1���ߡ�ACB��90����
��OBC+��OCB��90������ACO+��BCO��90�������OBC����ACO��
���COB�ס�AOC����OC2��OA��OB��3��
���C��0����![]() �������ACO��30����
�������ACO��30����
����κ�������ʽΪ��y��a��x+1����x��3����a��x2��2x��3����
������3a����![]() ����a��
����a��![]() ��
��
�������ߵı���ʽΪ��![]() ��
��
��2����C��0����![]() ������B��0��3����
������B��0��3����
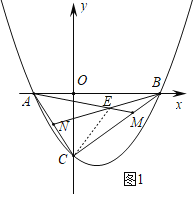
��CM��2BM����M��2��![]() ����
����
����CE������N��AC���е㣬
��S��ABN��S��CBN��S��AEN��S��CEN��
��S��EBA��S��EBC��
�裺S��BEM��S����CM��2BM��S��CBE��3S��S��EBA��
��S��BEM��S��![]() S��ABM��
S��ABM��![]() ��
��![]() ��
��
��3���ܣ����ɣ�
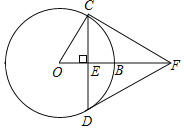
��ͼ2������C����x���ƽ���߽�����O����y���ƽ�����ڵ�H��
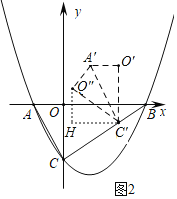
�ߡ�AOC��30�������O��C��H��30����������HC��O����90����
����B��C���������һ�κ�������ʽ��y��kx+b����ã�
ֱ��BC�ı���ʽΪ��![]() ��
��
���C����n��![]() ������HC����C��O��cos30����
������HC����C��O��cos30����![]() ��
��
HO����![]() �����O����
�����O����![]() ��
��![]() ����
����
��O��C��2��3��AO��2��![]() +
+![]() 2��AC��2����n+1��2+
2��AC��2����n+1��2+![]()
�ٵ�O��C����AO��ʱ��3��![]() +
+![]() ����ã�
����ã�![]() ��
��
�ڵ�O��C����AC��ʱ���⣻
�۵�AO����AC��ʱ��ͬ���ɵã�![]() ��
��
�ʵ�C������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����