题目内容
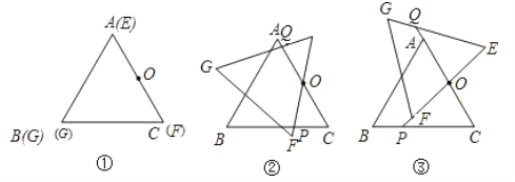
【题目】如图,在△ABD中,AB=AD,AB是⊙O的直径,DA、DB分别交⊙O于点E、C,连接EC,OE,OC.
(1)当∠BAD是锐角时,求证:△OBC≌△OEC;
(2)填空:
①若AB=2,则△AOE的最大面积为 ;
②当DA与⊙O相切时,若AB=![]() ,则AC的长为 .
,则AC的长为 .
【答案】(1)见解析;(2)①S△AOE最大=![]() ;②AC=1.
;②AC=1.
【解析】
(1)利用垂直平分线,判断出∠BAC=∠DAC,得出EC=BC,用SSS判断出结论;
(2)①先判断出三角形AOE面积最大,只有点E到直径AB的距离最大,即是圆的半径即可;②根据切线的性质和等腰直角三角形的性质解答即可.
(1)连接AC,如图1,
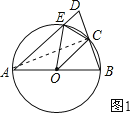
∵AB是⊙O的直径,
∴AC⊥BD,
∵AD=AB,
∴∠BAC=∠DAC,
∴![]() ,
,
∴BC=EC,
在△OBC和△OEC中 ,
,
∴△OBC≌△OEC(SSS),
(2)①∵AB是⊙O的直径,且AB=2,
∴OA=1,
设△AOE的边OA上的高为h,
∴S△AOE=![]() OA×h=
OA×h=![]() ×1×h=
×1×h=![]() h,
h,
∴要使S△AOE最大,只有h最大,
∵点E在⊙O上,
∴h最大是半径,
即h最大=1
∴S△AOE最大=![]() ,
,
故答案为![]() ;
;
②如图2:
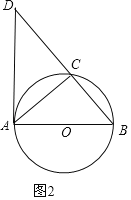
当DA与⊙O相切时,
∴∠DAB=90°,
∵AD=AB=![]() ,
,
∴∠ABD=45°,
∵AB是直径,
∴∠ADB=90°,
∴AC=BC=![]() ,
,
故答案为1

【题目】某公司购进一批新产品进行销售,已知该产品的进货单价为8元/件,该公司对这批新产品上市后的销售情况进行了跟踪调查.销售过程中发现,该产品每月的销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系满足下表.
(元)之间的关系满足下表.
销售单价 | … | 10 | 12 | 14 | 15 | … |
每月销售量 | … | 40 | 36 | 32 | 30 | … |
(1)请你从所学过的一次函数、二次函数和反比例函数三个模型中确定哪种函数能比较恰当地表示![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当销售单价为多少元时,该产品每月获得的利润为240万元?
(3)如果该产品每月的进货成本不超过160万元,那么当销售单价为多少元时,该产品每月获得的利润最大?最大利润为多少万元?