题目内容
【题目】在△ABC中,AB=![]() ,BC=6,∠B=45°,D为BC边上一点将△ABC沿着过D点的直线折叠,使得点C落在AB边上,记CD=m,则AC=_____,m的取值范围是_____
,BC=6,∠B=45°,D为BC边上一点将△ABC沿着过D点的直线折叠,使得点C落在AB边上,记CD=m,则AC=_____,m的取值范围是_____
【答案】![]()
![]()
【解析】
过A点作AN⊥BC于点N,由等腰直角三角形的性质得出AN=BN=4,求出CN=BC﹣BN=2,在Rt△ANC中,由勾股定理即可得出AC的长;
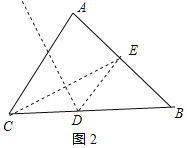
①当DE⊥AB时,DE最小,即CD最小,根据已知条件得到△DEB是等腰直角三角形,设CD=DE=x,则DE=EB=x,∠DEB=90°,DB=![]() x,解直角三角形得到结论,②如图2中,当E与A重合时,DE最大,即CD最大,作AH⊥CB于H,设CD=DE=x,在Rt△AHB中,易知AH=HB=4,∠AHB=90°,HD=x﹣2,DE=x,根据勾股定理即可得到结论.
x,解直角三角形得到结论,②如图2中,当E与A重合时,DE最大,即CD最大,作AH⊥CB于H,设CD=DE=x,在Rt△AHB中,易知AH=HB=4,∠AHB=90°,HD=x﹣2,DE=x,根据勾股定理即可得到结论.
解:过A点作AN⊥BC于点N,如图1所示:
∵∠B=45°,∠ANB=90°,
∴AN=BN=![]() AB=
AB=![]() ×
×![]() =4,
=4,
∴CN=BC﹣BN=2,
在Rt△ANC中,由勾股定理得:AC=![]() ;
;
①如图2所示,∵CD=DE,
∴当DE⊥AB时,DE最小,即CD最小,
∵∠B=45°,
∴△DEB是等腰直角三角形,
设CD=DE=x,则DE=EB=x,∠DEB=90°,DB=![]() x,
x,
∵BC=6,
∴x+![]() x=6,
x=6,
∴x=6![]() ﹣6,
﹣6,
②如图3所示,当E与A重合时,
作AH⊥CB于H,设CD=DE=x,
在Rt△AHB中,AH=HB=4,∠AHB=90°,HD=x﹣2,DE=x,
∴x2=42+(x﹣2)2,
∴x=5,
综上可知,CD的最大值为5,最小值为6![]() ﹣6,
﹣6,
∴CD的取值范围是6![]() ﹣6≤CD≤5,
﹣6≤CD≤5,
故答案为:![]() ,6
,6![]() ﹣6≤m≤5.
﹣6≤m≤5.



练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目