题目内容
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.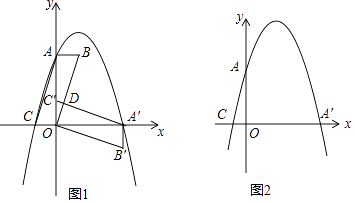
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.
【答案】
(1)
解:如图1中,
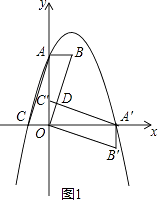
∵平行四边形ABOC绕点O顺时针旋转90°,得到平行四边
形A′B′OC′,点A的坐标是(0,4),
∴点A′的坐标为(4,0).
∵抛物线过点C,A,A′,设抛物线的函数解析式为
y=ax2+bx+c(a≠0)可得:
 ,解得:
,解得: 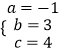 ,
,
∴抛物线的函数解析式为y=﹣x2+3x+4.
(2)
解:如图2中,连接AA′,设直线AA′的函数解析式为y=kx+b,
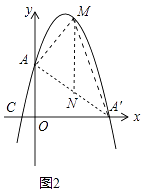
可得: ![]() ,解得:
,解得: ![]() ,
,
∴直线AA′的函数解析式是y=﹣x+4.
设M(x,﹣x2+3x+4),作MN∥y轴交AA′于N,则N(m,﹣m+4),
S△AMA′= ![]() ×4×[﹣x2+3x+4﹣(﹣x+4)]=﹣2(x﹣2)2+8,
×4×[﹣x2+3x+4﹣(﹣x+4)]=﹣2(x﹣2)2+8,
∵﹣2<0,
∴x=2时,△AMA′的面积最大,最大面积为8,
∴M(2,6).
(3)
解:如图3中,
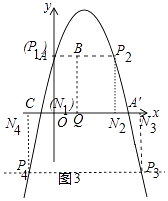
设P点的坐标为(x,﹣x2+3x+4),当P、N、B、Q构成平行四边形时,
①当BQ为边时,PN∥BQ 且PN=BQ,
∵BQ=4,
∴﹣x2+3x+4=±4.
当﹣x2+3x+4=4时,x=0或3,
可得P1(0,4),P2(3,4);
当﹣x2+3x+4=﹣4时,x= ![]() ,可得P3(
,可得P3( ![]() ,﹣4),P4(
,﹣4),P4( ![]() ,﹣4).
,﹣4).
②当BQ为对角线时,PB∥x轴,即P1,P2的坐标不变;
当这个平行四边形为矩形时,即P1(0,4),P2(3,4),N1(0,0),N2(3,0).
综上所述,当P1(0,4),P2(3,4),P3( ![]() ,﹣4),P4(
,﹣4),P4( ![]() ,﹣4).时,P、N、B、Q构成平行四边形;
,﹣4).时,P、N、B、Q构成平行四边形;
当这个平行四边形为矩形时,N1(0,0),N2(3,0).
【解析】(1)先确定C,A,A′三点坐标,利用待定系数法,转化为解方程组即可.(2)如图2中,连接AA′,设直线AA′的函数解析式为y=kx+b,设M(x,﹣x2+3x+4),作MN∥y轴交AA′于N,则N(m,﹣m+4),构建二次函数后利用二次函数的性质解决问题即可.(3)分两种情形讨论即可.①当BQ为边时,PN∥BQ 且PN=BQ,由BQ=4,可得﹣x2+3x+4=±4.解方程可以得到点P的横坐标.②当BQ为对角线时,PB∥x轴,即P1 , P2的坐标不变;当这个平行四边形为矩形时,点N的坐标利用图象即可解决.

 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案