Question

【题目】如图，在平面直角坐标系中，已知Rt△AOB的两直角边OA，OB分别在x轴，y轴的正半轴上（OA＜OB），且OA，OB的长分别是一元二次方程x2﹣14x+48=0的两个根，线段AB的垂直平分线CD交AB于点C，分别交x轴，y轴于点D，E．

（1）直接写出点A、B的坐标：A ， B；
（2）求线段AD的长；
（3）已知P是直线CD上一个动点，点Q是直线AB上一个动点，则在坐标平面内是否存在点M，使得以点C、P、Q、M为顶点的四边形是以5为边长的正方形？若存在，直接写出点M的坐标；若不存在，说明理由．

Answer 1

【答案】
（1）（6，0）；（0，8）
（2）

解：在Rt△AOB中，∵∠AOB=90°，OA=6，OB=8，

∴AB= =10，

∵线段AB的垂直平分线CD交AB于点C，

∴AC= AB=5．

在△ACD与△AOB中，

∵∠CAD=∠OAB，∠ACD=∠AOB=90°，

∴△ACD∽△AOB，

∴ = ，即 = ，

解得AD= ，

∵A（6，0），点D在x轴上，

∴D（﹣ ，0）．

设直线CD的解析式为y=kx+b，

由题意知C为AB中点，

∴C（3，4），

∵D（﹣ ，0），

∴ ，解得 ，

∴直线CD的解析式为y= x+ ；

（3）

解：在坐标平面内存在点M，使以点C、P、Q、M为顶点的四边形是正方形，且该正方形的边长为5，

∵AC=BC= AB=5，

∴以点C、P、Q、M为顶点的正方形的边长为5，且点Q与点B或点A重合．分两种情况：

① 当点Q与点B重合时，易求BM的解析式为y= x+8，设M（x， x+8），

∵B（0，8），BM=5，

∴（ x+8﹣8）2+x2=52，

化简整理，得x2=16，

解得x=±4，

∴M2（4，11），M3（﹣4，5）；

②当点Q与点A重合时，易求AM的解析式为y= x﹣ ，

设M（x， x﹣ ），

∵A（6，0），AM=5，

∴（ x﹣ ）2+（x﹣6）2=52，

化简整理，得x2﹣12x+20=0，

解得x1=2，x2=10，

∴M4（2，﹣3），M1（10，3）；

综上所述，所求点M的坐标为M1（10，3），M2（4，11），M3（﹣4，5），M4（2，﹣3）．

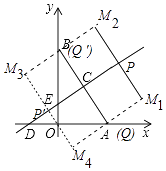
【解析】解：（1）解方程x2﹣14x+48=0，
得x1=6，x2=8，
∵OA＜OB，
∴A（6，0），B（0，8）；
所以答案是（6，0），（0，8）．
【考点精析】掌握相似三角形的判定是解答本题的根本，需要知道相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）．