��Ŀ����
����Ŀ��ij�մɹ�˾�й����ƣ�������˾���˹���ʱ�䣺ÿ�칤��![]() Сʱ��ÿ�¹���
Сʱ��ÿ�¹���![]() �죻���������˰��Ƽ������ʣ�ÿ�����������
�죻���������˰��Ƽ������ʣ�ÿ�����������![]() Ԫ�����½����������ù�˾ֻ�����ס��������մɣ�����С����¼������һЩ���ݣ�
Ԫ�����½����������ù�˾ֻ�����ס��������մɣ�����С����¼������һЩ���ݣ�
�����մ� ����λ������ | �����մ� ����λ������ | ��ʱ�� ����λ�����ӣ� | �Ƽ����� ����λ��Ԫ�� |
|
|
|
|
|
|
|
|
��1��������ÿ�������մ������ʱ��Ϊ![]() ���ӣ��ú���
���ӣ��ú���![]() �Ĵ���ʽ��ʾ����ÿ�������մ������ʱ�䣻
�Ĵ���ʽ��ʾ����ÿ�������մ������ʱ�䣻
��2����С������С��ij�£�����![]() �죩���������մ�
�죩���������մ�![]() ���������մ�
���������մ�![]() ����
����
������![]() ��
��![]() �ĺ�����ϵʽ��������д���Ա���
�ĺ�����ϵʽ��������д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�ڸ����г����飬ÿ������ÿ�����������մɵ����������������մ�������![]() ����������ÿ�������մɵļƼ����ʿ����
����������ÿ�������մɵļƼ����ʿ����![]() Ԫ�������մɼƼ�����Ҳ����ߵĿռ䣮��С���Ĺ���Ч�ʲ��䣬�����մɼƼ���������Ҫ��߶���Ԫ��С�����¹��ʣ��Ƽ�����+��������
Ԫ�������մɼƼ�����Ҳ����ߵĿռ䣮��С���Ĺ���Ч�ʲ��䣬�����մɼƼ���������Ҫ��߶���Ԫ��С�����¹��ʣ��Ƽ�����+��������![]() �¹��ʣ������쵽
�¹��ʣ������쵽![]() Ԫ��
Ԫ��
���𰸡�(1) ��35-m�����ӣ�(2)��y=![]() x+600���ڼ����մɼƼ���������Ҫ���0.3Ԫ��С�����¹��ʲ����쵽1200Ԫ��
x+600���ڼ����մɼƼ���������Ҫ���0.3Ԫ��С�����¹��ʲ����쵽1200Ԫ��
��������
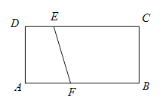
��1�����������֪������ÿ�������մ�����ʱ��Ϊ��35-m�����ӣ�
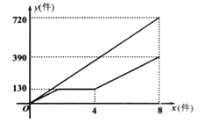
��2�������ȸ���ͼ�����з��������һ�������մ��������մɵ�ʱ�䣬�ٸ���һ�µĹ���ʱ�伴����ú�������ʽ��
��������ÿ�������մɼƼ�����ΪaԪ������ÿ�������մɼƼ�����ΪbԪ�����ù���2.8��6.6��Ϊ��ȹ�ϵ�з����飬���![]() ���Ӷ��õ�p��
���Ӷ��õ�p��![]() �����ݷ����������ĵ����Կ�֪��p��x������������������x��500����x=500ʱ��pȡ����Сֵ����ʱp=0.3��
�����ݷ����������ĵ����Կ�֪��p��x������������������x��500����x=500ʱ��pȡ����Сֵ����ʱp=0.3��
��1������ÿ�������մ�����ʱ��Ϊ��35-m�����ӣ�
��2�����������֪��3m+2��35-m��=85
��ã�m=15
������ÿ�������մ�����ʱ�䣺35-m=20����
�������֪��15x+20y=8��25��60
����ã�y=![]() x+600
x+600
��y��x�ĺ�����ϵʽ��y=![]() x+600��
x+600��
��������ÿ�������մɼƼ�����ΪaԪ������ÿ�������մɼƼ�����ΪbԪ��
�������֪��![]() ����ã�
����ã�![]() ��
��
������մɼƼ�����Ҫ���pԪ��С�����¹��ʲ����쵽1200Ԫ
�������֪��1200��(1+p)x+(1.8+0.2)( ![]() x+600)+100
x+600)+100
����ã�p��![]()
��p��![]() �Ƿ�������������k=100��0
�Ƿ�������������k=100��0
��p��x���������С
����p��![]() ��p��x�����������
��p��x�����������
�֡�x��![]() y��x��
y��x��![]() (
(![]() x+600)
x+600)
��ã�x��500
�൱x=500ʱ��pȡ�����ֵ����ʱp=0.3��
�𣺼����մɼƼ���������Ҫ���0.3Ԫ��С�����¹��ʲ����쵽1200Ԫ��

 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д�