题目内容
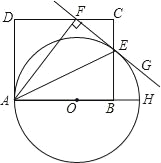
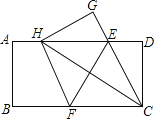
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①HE=HF;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2![]() .以上结论中,你认为正确的有( )个.
.以上结论中,你认为正确的有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题分析:∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,由翻折的性质得,CF=FH,∴四边形CFHE是菱形,∴①正确;
∴∠BCH=∠ECH,∴只有∠DCE=30°时EC平分∠DCH,∴②错误;
点H与点A重合时,设BF=x,则AF=FC=8-x,在Rt△ABF中,![]() ,
,
即![]() ,解得x=3,点G与点D重合时,CF=CD=4, ∴BF=4,
,解得x=3,点G与点D重合时,CF=CD=4, ∴BF=4,
∴线段BF的取值范围为3≤BF≤4,∴③正确;
过点F作FM⊥AD于M,则ME=(8-3)-3=2,由勾股定理得EF=2![]() ,∴④正确;
,∴④正确;

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目