Question

【题目】经过点A（4，1）的直线与反比例函数y＝的图象交于点A、C，AB⊥y轴，垂足为B，连接BC．

（1）求反比例函数的表达式；

（2）若△ABC的面积为6，求直线AC的函数表达式；

（3）在（2）的条件下，点P在双曲线位于第一象限的图象上，若∠PAC＝90°，则点P的坐标是　 　．

Answer 1

【答案】（1）反比例函数的表达式为y＝（2）直线AC的函数表达式为y＝x﹣1；（3）（，8）．

【解析】

（1）将点A坐标代入反比例函数表达式中，即可得出结论；
（2）先求出AB，设出点C的纵坐标，利用△ABC的面积为6，求出点C纵坐标，再代入反比例函数表达式中，求出点C坐标，最后用待定系数法求出直线AC的解析式；
（3）先求出直线AP的解析式，再和反比例函数解析式联立求解即可得出结论．

解：（1）∵点A（4，1）在反比例函数y＝ 的图象上，

∴k＝4×1＝4，

∴反比例函数的表达式为y＝；

（2）设点C的纵坐标为m，

∵AB⊥y轴，A（4，1），

∴AB＝4，

∵△ABC的面积为6，

∴AB×（1﹣m）＝6，

∴m＝﹣2，

由（1）知，反比例函数的表达式为y＝，

∴点C的纵坐标为：﹣2，

∴点C（﹣2，﹣2），

设直线AC的解析式为y＝k'x+b，

将点A（4，1），C（﹣2，﹣2）代入y＝k'x+b中， ，

∴ ，

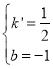∴直线AC的函数表达式为y＝x﹣1；

（3）由（2）知直线AC的函数表达式为y＝x﹣1，

∵∠PAC＝90°，

∴AC⊥AP，

∴设直线AP的解析式为y＝﹣2x+b'，

将A（4，1）代入y＝﹣2x+b'中，﹣8+b'＝1，

∴b'＝9，

∴直线AP的解析式为y＝﹣2x+9①，

由（1）知，反比例函数的表达式为y＝②，

联立①②解得， （舍）或 ，

∴点P的坐标为（，8），

故答案为：（，8）．