Question

【题目】已知二次函数y＝x2+bx+c.

(Ⅰ)若二次函数的图象经过(3，﹣2)，且对称轴为x＝1，求二次函数的解析式；

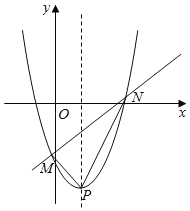
(Ⅱ)如图，在(Ⅰ)的条件下，过定点的直线y＝﹣kx+k﹣4(k≤0)与(1)中的抛物线交于点M，N，且抛物线的顶点为P，若△PMN的面积等于3，求k的值；

(Ⅲ)当c＝b2时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式.

Answer 1

【答案】(Ⅰ)y＝x2﹣2x﹣5；(Ⅱ)k=2；(Ⅲ)y＝x2﹣4x+16或y＝x2+x+7.

【解析】

(Ⅰ)根据题意得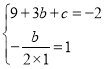，，解得：，即可求解；

(Ⅱ)△PMN的面积S＝S△PGN﹣S△PGM＝GP(xN﹣xM)＝xN﹣xM＝＝3，即可求解；

(Ⅲ)分b+3≤﹣(即b≤﹣2)、b≥﹣(即b≥0)、﹣2＜b＜0三种情况，分别求解即可.

(Ⅰ)根据题意得，，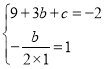

解得：，

∴二次函数的解析式为y＝x2﹣2x﹣5…①；

(Ⅱ)如图1，

∵y＝﹣kx+k﹣4＝﹣k(x﹣1)﹣4…②，

联立①②并整理得：x2﹣(2﹣k)x﹣k﹣1＝0，

则xM+xN＝2﹣k，xMxN＝﹣k﹣1，

xN﹣xM＝＝；

∴当x＝1时，y＝﹣4，即该直线所过定点G坐标为(1，﹣4)，

∵y＝x2﹣2x﹣5＝(x﹣1)2﹣6，

∴点P(1，﹣6)，

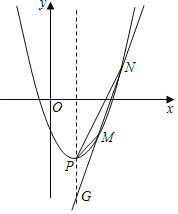
△PMN的面积S＝S△PGN﹣S△PGM＝GP(xN﹣xM)＝xN﹣xM＝＝3，

解得：k＝±2(舍去2)，故k＝﹣2；

(Ⅲ)抛物线的表达式为：y＝x2+bx+b2，

抛物线的对称轴为x＝﹣；

①当b+3≤﹣(即b≤﹣2)时，

则x＝b+3时，函数取得最小值，

即(b+3)2+b(b+3)+b2＝21，

解得：b＝﹣4或1(舍去1)；

②当b≥﹣(即b≥0)时，

则x＝b时，函数取得最小值，

即b2+b2+b2＝21，解得：b＝(舍去负值)；

③当﹣2＜b＜0时，

则﹣b2+b2＝21，解得：b＝±2(舍去)；

综上，b＝﹣4或，

故抛物线的表达式为：y＝x2﹣4x+16或y＝x2+x+7.