题目内容
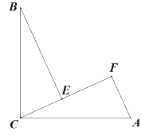
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是四边形内一点,若S四边形AEOH=3,S四边形BFOE=4,S四边形CGOF=5,则S四边形DHOG= . 
【答案】4
【解析】解:连接OC,OB,OA,OD,
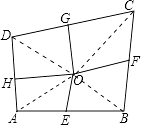
∵E、F、G、H依次是各边中点,
∴△AOE和△BOE等底等高,所以S△OAE=S△OBE,
同理可证,S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE,
∵S四边形AEOH=3,S四边形BFOE=4,S四边形CGOF=5,
∴3+5=4+S四边形DHOG,
解得,S四边形DHOG=4.
故应填4.
【考点精析】掌握三角形的面积是解答本题的根本,需要知道三角形的面积=1/2×底×高.

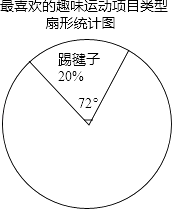
【题目】某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳长绳 | 25 | a |
踢毽子 | 20 | 0.2 |
背夹球 | b | 0.4 |
拔河 | 15 | 0.15 |
(1)直接写出a= , b=;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术字画 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= , b=;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?