题目内容
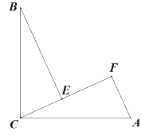
【题目】如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0＜∠ACF＜45°.
(1)求证:△BEC≌△CEA；
(2)若AF=5,EF=8,求BE的长.
【答案】(1)见解析(2) 13
【解析】
（1）由余角的性质可得∠B=∠ACF，即可证△BEC≌△CFA；
（2）由全等三角形的性质可求解．
证明：（1）∵BE⊥CF，∠BCA=90°，
∴∠B+∠BCE=90°，∠BCE+∠ACF=90°，
AF⊥CF∠B=∠ACF，
∵BE⊥CF，AF⊥CF
∴∠BEC=∠AFC=90°
在△BEC和△CFA中
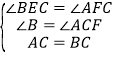
∴△BEC≌△CFA；
（2）∵△BEC≌△CFA
∴CE=AF=5，BE=CF，
∵FC=CE+EF=5+8=13
∴BE=13
练习册系列答案
孟建平名校考卷系列答案
相关题目
【题目】某校在艺术节宣传活动中，采用了四种宣传形式：A唱歌，B舞蹈，C朗诵，D器乐．全校的每名学生都选择了一种宣传形式参与了活动，小明对同学们选用的宣传形式，进行了随机抽样调查，根据调查统计结果，绘制了如图两种不完整的统计图表：
选项 | 方式 | 百分比 |
A | 唱歌 | 35% |
B | 舞蹈 | a |
C | 朗诵 | 25% |
D | 器乐 | 30% |
请结合统计图表，回答下列问题：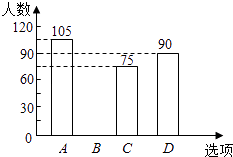
（1）本次调查的学生共人，a= ， 并将条形统计图补充完整 ；
（2）如果该校学生有2000人，请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人？
（3）学校采用调查方式让每班在A、B、C、D四种宣传形式中，随机抽取两种进行展示，请用树状图或列表法，求某班抽到的两种形式有一种是“唱歌”的概率．
