题目内容
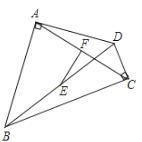
【题目】如图1,直线y=﹣![]() x+6与y轴于点A,与x轴交于点D,直线AB交x轴于点B,△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
x+6与y轴于点A,与x轴交于点D,直线AB交x轴于点B,△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
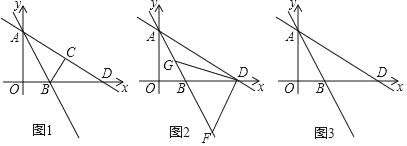
(1)求点B的坐标;
(2)如图2,直线AB上的两点F、G,△DFG是以FG为斜边的等腰直角三角形,求点G的坐标;
(3)如图3,点P是直线AB上一点,点Q是直线AD上一点,且P、Q均在第四象限,点E是x轴上一点,若四边形PQDE为菱形,求点E的坐标.
【答案】(1)B(3,0)(2)G(2,2);(3)E(﹣2,0).
【解析】
(1)根据题意可先求出点A和点D的坐标,然后根据勾股定理求出AD,设BC=OB=x,则BD=8-x,在直角三角形BCD中根据勾股定理求出x,即可得到点B的坐标;
(2)由点A和点B的坐标可先求出AB的解析式,然后作GM⊥x轴于M,FN⊥x轴于N,求证△DMG≌△FND,从而得到GM=DN,DM=FN,又因为G、F在直线AB上,进而可求点G的坐标;
(3)设点Q(a,-![]() a+6),则点P的坐标为(
a+6),则点P的坐标为(![]() a,-
a,-![]() a+6),据此可求出PQ,作QH⊥x轴于H,可以把QH用a表示出来,在直角三角形中,根据勾股定理也可以用a把QH表示出来,从而求出a的值,进而求出点E的坐标.
a+6),据此可求出PQ,作QH⊥x轴于H,可以把QH用a表示出来,在直角三角形中,根据勾股定理也可以用a把QH表示出来,从而求出a的值,进而求出点E的坐标.
解:(1)对于直线y=-![]() x+6,令x=0,得到y=6,可得A(0,6),
x+6,令x=0,得到y=6,可得A(0,6),
令y=0,得到x=8,可得D(8,0),
∴AC=AO=6,OD=8,AD=![]() =10,
=10,
∴CD=AD﹣AC=4,设BC=OB=x,则BD=8﹣x,
在Rt△BCD中,∵BC2+CD2=BD2,
∴x2+42=(8﹣x)2,
∴x=3,
∴B(3,0).
(2)设直线AB的解析式为y=kx+6,
∵B(3,0),
∴3k+6=0,
∴k=﹣2,
∴直线AB的解析式为y=﹣2x+6,
作GM⊥x轴于M,FN⊥x轴于N,
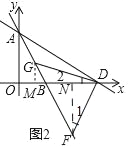
∵△DFG是等腰直角三角形,
∴DG=FD,∠1=∠2,∠DMG=∠FND=90°,
∴△DMG≌△FND(AAS),
∴GM=DN,DM=FN,设GM=DN=m,DM=FN=n,
∵G、F在直线AB上,
∴![]() ,
,
解得![]() ,
,
∴G(2,2).
(3)如图,设Q(a,﹣![]() a+6),
a+6),
∵PQ∥x轴,且点P在直线y=﹣2x+6上,
∴P(![]() a,﹣
a,﹣![]() a+6),
a+6),
∴PQ=![]() a,作QH⊥x轴于H,
a,作QH⊥x轴于H,
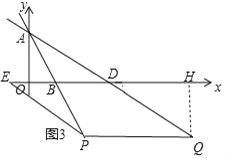
∴DH=a﹣8,QH=![]() a﹣6,
a﹣6,
∴![]() =
=![]() ,
,
由勾股定理可知:QH:DH:DQ=3:4:5,
∴QH=![]() DQ=
DQ=![]() PQ=
PQ=![]() a,
a,
∴![]() a=
a=![]() a﹣6,
a﹣6,
∴a=16,
∴Q(16,﹣6),P(6,﹣6),
∵ED∥PQ,ED=PQ,D(8,0),
∴E(﹣2,0).

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
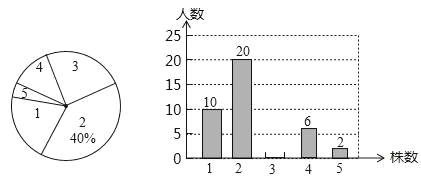
启东小题作业本系列答案【题目】某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
选项 | 方式 | 百分比 |
A | 唱歌 | 35% |
B | 舞蹈 | a |
C | 朗诵 | 25% |
D | 器乐 | 30% |
请结合统计图表,回答下列问题: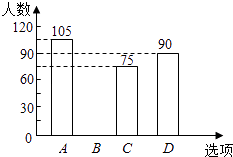
(1)本次调查的学生共人,a= , 并将条形统计图补充完整 ;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.