题目内容
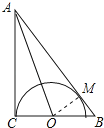
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠CAO= ![]() ,求cosB的值.
,求cosB的值.
【答案】
(1)
解:如图作OM⊥AB于M,
∵OA平分∠CAB,OC⊥AC,OM⊥AB,
∴OC=OM,
∴AB是⊙O的切线,
(2)
解:设BM=x,OB=y,则y2﹣x2=1 ①,
∵cosB= ![]() ,
,
∴ ![]() ,
,
∴x2+3x=y2+y ②,
由①②可以得到:y=3x﹣1,
∴(3x﹣1)2﹣x2=1,
∴x= ![]() ,y=
,y= ![]() ,
,
∴cosB= ![]() =
= ![]() .
.
【解析】(1)如图作OM⊥AB于M,根据角平分线性质定理,可以证明OM=OC,由此即可证明.(2)设BM=x,OB=y,列方程组即可解决问题.本题考查切线的判定、勾股定理、三角函数等知识,解题的关键是记住圆心到直线的距离等于半径,这条直线就是圆的切线,学会设未知数列方程组解决问题,属于中考常考题型.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对锐角三角函数的定义的理解,了解锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目