Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ“—÷™Ň◊őÔŌŖy=x2+bx+cĺ≠ĻżA£®©Ā1£¨0£©£¨B£®3£¨0£©ŃĹĶ„£¨”Žy÷ŠŌŗĹĽ”ŕĶ„C£¨ł√Ň◊őÔŌŖĶń∂•Ķ„ő™Ķ„D
£®1£©«ůł√Ň◊őÔŌŖĶńĹ‚őŲ ĹľįĶ„DĶń◊ÝĪÍ°£
£®2£©Ń¨Ĺ”AC£¨CD£¨BD£¨BC£¨…Ť°ųAOC£¨°ųBOC£¨°ųBCDĶń√śĽż∑÷Īūő™S1 £¨ S2ļÕS3 £¨ ”√Ķ» ĹĪŪ ĺS1 £¨ S2 £¨ S3÷ģľšĶń żŃŅĻōŌĶ£¨≤ĘňĶ√ųņŪ”…
£®3£©ľŔ…Ťīś‘ŕ£¨…ŤĶ„MĶń◊ÝĪÍő™£®m£¨0£©£¨ĪŪ ĺ≥ŲMAĶń≥§£¨łýĺ›MN°őBC£¨Ķ√ĶĹĪ»ņż Ĺ«ů≥ŲAN£¨łýĺ›°ųAMN°◊°ųACM£¨Ķ√ĶĹĪ»ņż Ĺ«ů≥Ųm£¨Ķ√ĶĹĶ„MĶń◊ÝĪÍ£¨«ů≥ŲBCĶńĹ‚őŲ Ĺ£¨łýĺ›MN°őBC£¨…Ť÷ĪŌŖMNĶńĹ‚őŲ Ĺ£¨«ůĹ‚ľīŅ…
°ĺīūįł°Ņ
£®1£©
Ĺ‚£ļ°ŖŇ◊őÔŌŖy=x2+bx+cĺ≠ĻżA£®©Ā1£¨0£©£¨B£®3£¨0£©ŃĹĶ„£¨
°ŗ![]() £¨
£¨
Ĺ‚Ķ√![]() £ģ
£ģ
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™£ļy=x2©Ā2x©Ā3£¨
y=x2©Ā2x©Ā3=£®x©Ā1£©2©Ā4£¨
°ŗĶ„DĶń◊ÝĪÍő™£ļ£®1£¨©Ā4£©
£®2£©
Ĺ‚£ļS1+S3=S2£¨
ĻżĶ„D◊ųDE°Õx÷Š”ŕĶ„E£¨DF°Õy÷Š”ŕF£¨
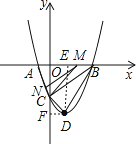
”…Ő‚“‚Ķ√£¨CD=![]() £¨BD=
£¨BD=![]() £¨BC=
£¨BC=![]() £¨
£¨
CD2+BC2=BD2£¨
°ŗ°ųBCD «÷ĪĹ«»żĹ«–ő£¨
S1=![]() °ŃOA°ŃOC=
°ŃOA°ŃOC=![]() £¨
£¨
S2=![]() °ŃOB°ŃOC=
°ŃOB°ŃOC=![]()
S3=![]() °ŃCD°ŃBC=3£¨
°ŃCD°ŃBC=3£¨
°ŗS1+S3=S2
£®3£©
Ĺ‚£ļīś‘ŕĶ„M Ļ°ŌAMN=°ŌACM£¨
…ŤĶ„MĶń◊ÝĪÍő™£®m£¨0£©£¨
°Ŗ©Ā1£ľm£ľ3£¨
°ŗMA=m+1£¨AC=![]() £¨
£¨
°ŖMN°őBC£¨
°ŗ![]() =
=![]() £¨ľī
£¨ľī![]() =
=![]() £¨
£¨
Ĺ‚Ķ√£¨AN=![]() £®m+1£©£¨
£®m+1£©£¨
°Ŗ°ŌAMN=°ŌACM£¨°ŌMAN=°ŌCAM£¨
°ŗ°ųAMN°◊°ųACM£¨
°ŗ![]() =
=![]() £¨ľī£®m+1£©2=
£¨ľī£®m+1£©2=![]()
![]() £®m+1£©£¨
£®m+1£©£¨
Ĺ‚Ķ√£¨m1=![]() £¨m2=©Ā1£®…Š»•£©£¨
£¨m2=©Ā1£®…Š»•£©£¨
°ŗĶ„MĶń◊ÝĪÍő™£®![]() £¨0£©£¨
£¨0£©£¨
…ŤBCĶńĹ‚őŲ Ĺő™y=kx+b£¨į—B£®3£¨0£©£¨C£®0£¨©Ā3£©īķ»ŽĶ√£¨
![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]() £¨
£¨
‘ÚBCĶńĹ‚őŲ Ĺő™y=x©Ā3£¨”÷MN°őBC£¨
°ŗ…Ť÷ĪŌŖMNĶńĹ‚őŲ Ĺő™y=x+b£¨į—Ķ„MĶń◊ÝĪÍő™£®![]() £¨0£©īķ»ŽĶ√£¨
£¨0£©īķ»ŽĶ√£¨
b=©Ā![]() £¨
£¨
°ŗ÷ĪŌŖMNĶńĹ‚őŲ Ĺő™y=x©Ā![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ£®1£©ņŻ”√īż∂®ŌĶ ż∑®«ů≥ŲŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£¨”√Ňš∑Ĺ∑®į—“Ľį„ ĹĽĮő™∂•Ķ„ Ĺ«ů≥ŲĶ„DĶń◊ÝĪÍ£Ľ
£®2£©łýĺ›Ķ„Ķń◊ÝĪÍ«ů≥Ų°ųAOC£¨°ųBOCĶń√śĽż£¨ņŻ”√ĻīĻ…∂®ņŪĶńńś∂®ņŪŇ–∂Ō°ųBCDő™÷ĪĹ«»żĹ«–ő£¨«ů≥Ų∆š√śĽż£¨ľ∆ň„ľīŅ…Ķ√ĶĹīūįł£Ľ
£®3£©ľŔ…Ťīś‘ŕ£¨…ŤĶ„MĶń◊ÝĪÍő™£®m£¨0£©£¨ĪŪ ĺ≥ŲMAĶń≥§£¨łýĺ›MN°őBC£¨Ķ√ĶĹĪ»ņż Ĺ«ů≥ŲAN£¨łýĺ›°ųAMN°◊°ųACM£¨Ķ√ĶĹĪ»ņż Ĺ«ů≥Ųm£¨Ķ√ĶĹĶ„MĶń◊ÝĪÍ£¨«ů≥ŲBCĶńĹ‚őŲ Ĺ£¨łýĺ›MN°őBC£¨…Ť÷ĪŌŖMNĶńĹ‚őŲ Ĺ£¨«ůĹ‚ľīŅ…£ģ
°ĺŅľĶ„ĺęőŲ°ŅĹ‚īūīňŐ‚ĶńĻōľŁ‘ŕ”ŕņŪĹ‚Ōŗň∆»żĹ«–őĶń–‘÷ ĶńŌŗĻō÷™ ∂£¨’∆ő’∂‘”¶Ĺ«ŌŗĶ»£¨∂‘”¶ĪŖ≥…Ī»ņżĶńŃĹłŲ»żĹ«–őĹ–◊ŲŌŗň∆»żĹ«–ő£ģ







