Question

【题目】如图1，△ABC和△DEF中，AB=AC，DE=DF，∠A=∠D．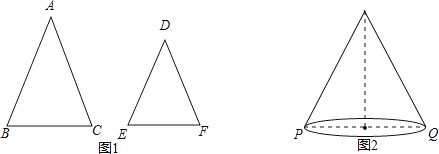

（1）求证： ；
（2）由（1）中的结论可知，等腰三角形ABC中，当顶角∠A的大小确定时，它的对边（即底边BC）与邻边（即腰AB或AC）的比值也就确定，我们把这个比值记作T（A），即T（A）= 的对边（底边）/的领边（腰）= ，如T（60°）=1．
①理解巩固：T（90°）= ， T（120°）= ， 若α是等腰三角形的顶角，则T（α）的取值范围是；
②学以致用：如图2，圆锥的母线长为9，底面直径PQ=8，一只蚂蚁从点P沿着圆锥的侧面爬行到点Q，求蚂蚁爬行的最短路径长（精确到0.1）．
（参考数据：T（160°）≈1.97，T（80°）≈1.29，T（40°）≈0.68）

Answer 1

【答案】
（1）

证明：∵AB=AC，DE=DF，

∴ ，

又∵∠A=∠D，

∴△ABC∽△DEF，

∴

（2）；；0＜T（α）＜2
【解析】（2）①如图1，

∠A=90°，AB=AC，
则 = ，
∴T（90°）= ，
如图2，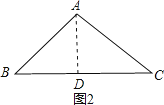

∠A=90°，AB=AC，
作AD⊥BC于D，
则∠B=60°，
∴BD= AB，
∴BC= AB，
∴T（120°）= ；
∵AB﹣AC＜BC＜AB+AC，
∴0＜T（α）＜2，
所以答案是： ； ；0＜T（α）＜2；
②∵圆锥的底面直径PQ=8，
∴圆锥的底面周长为8π，即侧面展开图扇形的弧长为8π，
设扇形的圆心角为n°，
则 =8π，
解得，n=160，
∵T（160°）≈1.97，
∴蚂蚁爬行的最短路径长为1.97×9≈17.7．
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点，需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．