��Ŀ����
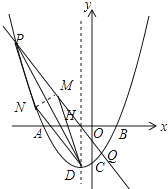
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=a��x+1��2��3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��0���� ![]() ��������ΪD���Գ�����x�ύ�ڵ�H������H��ֱ��l����������P��Q���㣬��Q��y����Ҳ࣮
��������ΪD���Գ�����x�ύ�ڵ�H������H��ֱ��l����������P��Q���㣬��Q��y����Ҳ࣮ 
��1����a��ֵ����A��B�����ꣻ
��2����ֱ��l���ı���ABCD��Ϊ�����Ϊ3��7��������ʱ����ֱ��l�ĺ�������ʽ��
��3������Pλ�ڵڶ�����ʱ����PQ���е�ΪM����N���������ϣ�����DPΪ�Խ��ߵ��ı���DMPN�ܷ�Ϊ���Σ����ܣ������N�����ꣻ�����ܣ���˵�����ɣ�
���𰸡�
��1��
�⣺����������y�ύ�ڵ�C��0���� ![]() ����
����
��a��3=�� ![]() ����ã�a=
����ã�a= ![]() ��
��
��y= ![]() ��x+1��2��3
��x+1��2��3
��y=0ʱ���� ![]() ��x+1��2��3=0��
��x+1��2��3=0��
��x1=2��x2=��4��
��A����4��0����B��2��0��
��2��
�⣺��A����4��0����B��2��0����C��0���� ![]() ����D����1����3��
����D����1����3��
��S�ı���ABCD=S��ADH+S����OCDH+S��BOC= ![]() ��3��3+
��3��3+ ![]() ��
�� ![]() +3����1+
+3����1+ ![]() ��2��
��2�� ![]() =10��
=10��
���������֪��ֱ��lֻ�����AD��BC�ཻ�����������������
�ٵ�ֱ��l��AD�ཻ���M1ʱ���� ![]() =
= ![]() ��10=3��
��10=3��
�� ![]() ��3������
��3������ ![]() ��=3
��=3
�� ![]() =��2����M1����2����2��������H����1��0����M1����2����2����ֱ��l�Ľ���ʽΪy=2x+2��
=��2����M1����2����2��������H����1��0����M1����2����2����ֱ��l�Ľ���ʽΪy=2x+2��
�ڵ�ֱ��l��BC�ཻ���M2ʱ��ͬ���ɵõ�M2�� ![]() ����2��������H����1��0����M2��
����2��������H����1��0����M2�� ![]() ����2����ֱ��l�Ľ���ʽΪy=��
����2����ֱ��l�Ľ���ʽΪy=�� ![]() x��
x�� ![]() ��
��
����������ֱ��l�ĺ�������ʽΪy=2x+2��y=�� ![]() x��
x�� ![]()
��3��
�⣺��P��x1��y1����Q��x2��y2���ҹ���H����1��0����ֱ��PQ�Ľ���ʽΪy=kx+b��
�ੁk+b=0��
��b=k��
��y=kx+k��
��  ��
��
�� ![]() +��
+�� ![]() ��k��x��
��k��x�� ![]() ��k=0��
��k=0��
��x1+x2=��2+3k��y1+y2=kx1+k+kx2+k=3k2��
�ߵ�M���߶�PQ���е㣬�����е����깫ʽ�ĵ�M�� ![]() k��1��
k��1�� ![]() k2����
k2����
�������������N����ͼ��ֱ��DN��PQ����ֱ��DN�Ľ���ʽΪy=kx+k��3
�� 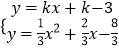 ����ã�x1=��1��x2=3k��1����N��3k��1��3k2��3��
����ã�x1=��1��x2=3k��1����N��3k��1��3k2��3��
���ı���DMPN�����Σ�
��DN=DM��
�ࣨ3k��2+��3k2��2=�� ![]() ��2+��
��2+�� ![]() ��2��
��2��
�����ã�3k4��k2��4=0��
��k2+1��0��
��3k2��4=0��
���k=�� ![]() ��
��
��k��0��
��k=�� ![]() ��
��
��P����3 ![]() ��1��6����M����
��1��6����M���� ![]() ��1��2����N����2
��1��2����N����2 ![]() ��1��1��
��1��1��
��PM=DN=2 ![]() ��
��
��PM��DN��
���ı���DMPN��ƽ���ı��Σ�
��DM=DN��
���ı���DMPNΪ���Σ�
����DPΪ�Խ��ߵ��ı���DMPN�ܳ�Ϊ���Σ���ʱ��N������Ϊ����2 ![]() ��1��1����
��1��1����
����������1���ѵ�C���������߽���ʽ�������a����y=0���з��̼��������A��B���꣮��2��������ı���ABCD��������������Σ��ٵ�ֱ��l��AD�ཻ���M1ʱ������S��AHM1 = ![]() ��10=3�������M1���꼴�ɽ�����⣮�ڵ�ֱ��l��BC�ཻ���M2ʱ��ͬ���ɵõ�M2���꣮��3����P��x1 �� y1����Q��x2 �� y2���ҹ���H����1��0����ֱ��PQ�Ľ���ʽΪy=kx+b���õ�b=k�����÷����������M���꣬���ֱ��DN����ʽ�������÷����������N���꣬�г��������k�����ɽ�����⣮���⿼����κ����ۺ��⡢����ϵ������һ�κ��������ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ��������ۣ�ѧ�����ò���������⣬�÷��̵�˼��˼�����⣬�����п�ѹ���⣮
��10=3�������M1���꼴�ɽ�����⣮�ڵ�ֱ��l��BC�ཻ���M2ʱ��ͬ���ɵõ�M2���꣮��3����P��x1 �� y1����Q��x2 �� y2���ҹ���H����1��0����ֱ��PQ�Ľ���ʽΪy=kx+b���õ�b=k�����÷����������M���꣬���ֱ��DN����ʽ�������÷����������N���꣬�г��������k�����ɽ�����⣮���⿼����κ����ۺ��⡢����ϵ������һ�κ��������ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ��������ۣ�ѧ�����ò���������⣬�÷��̵�˼��˼�����⣬�����п�ѹ���⣮

 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�





