题目内容
【题目】阅读理解:在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() 与
与![]() 的“非常距离”,给出如下定义:
的“非常距离”,给出如下定义:
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ;
;
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() .
.
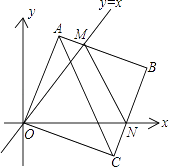
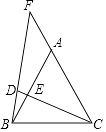
例如:点![]() ,点
,点![]() ,因为
,因为![]() ,所以点
,所以点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ,也就是图1中线段
,也就是图1中线段![]() 与线段
与线段![]() 长度的较大值(点
长度的较大值(点![]() 为垂直于
为垂直于![]() 轴的直线
轴的直线![]() 与垂直于
与垂直于![]() 轴的直线
轴的直线![]() 的交点).
的交点).
(1)已知点![]() ,
,![]() 为
为![]() 轴上的一个动点.
轴上的一个动点.
①若点![]() (0,3),则点
(0,3),则点![]() 与点
与点![]() 的“非常距离”为 ;
的“非常距离”为 ;
②若点![]() 与点
与点![]() 的“非常距离”为2,则点
的“非常距离”为2,则点![]() 的坐标为 ;
的坐标为 ;
③直接写出点![]() 与点
与点![]() 的“非常距离”的最小值为 ;
的“非常距离”的最小值为 ;
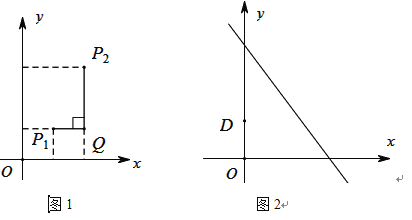
(2)已知点![]() (0,1),点
(0,1),点![]() 是直线
是直线![]() 上的一个动点,如图2,求点
上的一个动点,如图2,求点![]() 与点
与点![]() “非常距离”的最小值及相应的点
“非常距离”的最小值及相应的点![]() 的坐标.
的坐标.
【答案】(1)①3;②B(0,2)或(0,﹣2);③![]() ;(2)最小值为
;(2)最小值为![]() ,
, ![]() .
.
【解析】
(1)①根据若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() 解答即可;
解答即可;
②根据点B位于y轴上,可以设点B的坐标为![]() .由“非常距离”的定义可以确定
.由“非常距离”的定义可以确定![]() ,据此可以求得y的值;
,据此可以求得y的值;
③设点B的坐标为![]() .因为
.因为![]() ,所以点A与点B的“非常距离”最小值为
,所以点A与点B的“非常距离”最小值为![]() ;
;
(2)设点C的坐标为![]() .根据材料“若
.根据材料“若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ”,此时
”,此时![]() ,列出
,列出![]() 再求解,据此可以求得最小值和点C的坐标.
再求解,据此可以求得最小值和点C的坐标.
解:(1)① ![]() ,
,![]() .
.
∵ ![]() ,∴点A与点B的“非常距离”为3.
,∴点A与点B的“非常距离”为3.
② ∵B为y轴上的一个动点,∴设点B的坐标为(0,y).
∵![]() ,∴
,∴![]() .
.
解得,y=2或y=﹣2;
∴点B的坐标是(0,2)或(0,﹣2).
③ 点A与点B的“非常距离”的最小值为![]() .
.
(2)如图2,取点C与点D的“非常距离”的最小值时,
需要根据运算定义“若![]() ,则点
,则点![]() 与点
与点![]() 的‘非常距离’为
的‘非常距离’为![]() ”解答,此时
”解答,此时![]() .
.
∵![]() 是直线
是直线![]() 上的一个动点,点D的坐标是(0,1),
上的一个动点,点D的坐标是(0,1),
∴设点![]() 的坐标为
的坐标为![]() ,则
,则![]()
∴![]() 或
或![]() ,∴
,∴![]() 或
或![]() .
.
∵ ![]() ,∴点C与点D的“非常距离”的最小值为
,∴点C与点D的“非常距离”的最小值为![]() ,
,
此时![]() .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目