题目内容
【题目】如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
(1)求线段CD的长及顶点P的坐标;
(2)求抛物线的函数表达式;
(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB , 且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.
【答案】
(1)
解:如图,连接OC,
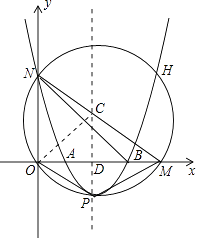
∵M(4,0),N(0,3),
∴OM=4,ON=3,
∴MN=5,
∴OC= ![]() MN=
MN= ![]() ,
,
∵CD为抛物线对称轴,
∴OD=MD=2,
在Rt△OCD中,由勾股定理可得CD= ![]() =
= ![]() =
= ![]() ,
,
∴PD=PC﹣CD= ![]() ﹣
﹣ ![]() =1,
=1,
∴P(2,﹣1);
(2)
解:∵抛物线的顶点为P(2,﹣1),
∴设抛物线的函数表达式为y=a(x﹣2)2﹣1,
∵抛物线过N(0,3),
∴3=a(0﹣2)2﹣1,解得a=1,
∴抛物线的函数表达式为y=(x﹣2)2﹣1,即y=x2﹣4x+3
(3)
解:在y=x2﹣4x+3中,令y=0可得0=x2﹣4x+3,解得x=1或x=3,
∴A(1,0),B(3,0),
∴AB=3﹣1=2,
∵ON=3,OM=4,PD=1,
∴S四边形OPMN=S△OMP+S△OMN= ![]() OMPD+
OMPD+ ![]() OMON=
OMON= ![]() ×4×1+
×4×1+ ![]() ×4×3=8=8S△QAB,
×4×3=8=8S△QAB,
∴S△QAB=1,
设Q点纵坐标为y,则 ![]() ×2×|y|=1,解得y=1或y=﹣1,
×2×|y|=1,解得y=1或y=﹣1,
当y=1时,则△QAB为钝角三角形,而△OBN为直角三角形,不合题意,舍去,
当y=﹣1时,可知P点即为所求的Q点,
∵D为AB的中点,
∴AD=BD=QD,
∴△QAB为等腰直角三角形,
∵ON=OB=3,
∴△OBN为等腰直角三角形,
∴△QAB∽△OBN,
综上可知存在满足条件的点Q,其坐标为(2,﹣1)
【解析】(1)连接OC,由勾股定理可求得MN的长,则可求得OC的长,由垂径定理可求得OD的长,在Rt△OCD中,可求得CD的长,则可求得PD的长,可求得P点坐标;(2)可设抛物线的解析式为顶点式,再把N点坐标代入可求得抛物线解析式;(3)由抛物线解析式可求得A、B的坐标,由S四边形OPMN=8S△QAB可求得点Q到x轴的距离,且点Q只能在x轴的下方,则可求得Q点的坐标,再证明△QAB∽△OBN即可.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案




