Question

【题目】如图，在中，，，，点从点沿向点以的速度运动，同时点从点沿向点以的速度运动（点运动到点停止），在运动的过程中，四边形的面积的最小值为__________．

Answer 1

【答案】15

【解析】

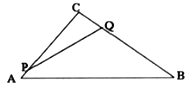
在Rt△ABC中，利用勾股定理可得出AC=6cm，设运动时间为t（0≤t≤4），则PC=（6-t）cm，CQ=2tcm，利用分割图形求面积法可得出S四边形PABQ=t2-6t+24，利用配方法即可求出四边形PABQ的面积最小值，此题得解．

在Rt△ABC中，∠C=90°，AB=10cm，BC=8cm，
∴AC==6cm．
设运动时间为t（0≤t≤4），则PC=（6-t）cm，CQ=2tcm，
∴S四边形PABQ=S△ABC-S△CPQ=ACBC-PCCQ=×6×8-（6-t）×2t=t2-6t+24=（t-3）2+15，
∴当t=3时，四边形PABQ的面积取最小值，最小值为15．
故答案为15．