Question

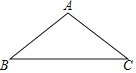
【题目】如图，已知△ABC中，AB＝AC＝5，BC＝8，若△ABC沿射线BC方向平移m个单位得到△DEF，顶点A，B，C分别与D，E，F对应，若以点A，D，E为顶点的三角形是等腰三角形，则m的值是_____．

Answer 1

【答案】或5或8．

【解析】

已知△ADE是等腰三角形，所以可以分3种情况讨论：①当AD＝AE时，△ADE是等腰三角形．作AM⊥BC，垂足为M，利用勾股定理列方程可得结论；②当AD＝DE时，四边形ABED是菱形，可得m＝5；③当AE＝DE时，此时C与E重合，m＝8．

解：分3种情况讨论：

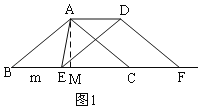
①当AD＝AE时，如图1，过A作AM⊥BC于M，

∵AB＝AC＝5，BM＝BC＝4，

∴AM＝3，

由平移得：AB∥DE，AB＝DE，

∴四边形ABED是平行四边形，

∴AD＝BE＝m，

∴AE＝m，EM＝4﹣m，

在Rt△AEM中，由勾股定理得：AE2＝AM2+EM2，

∴m2＝32+（4﹣m）2，

m＝，

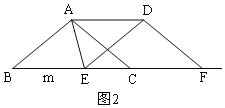
②当DE＝AE时，如图2，

同理得：四边形ABED是平行四边形，

∴AD＝BE＝ED＝AB＝5，

即m＝5；

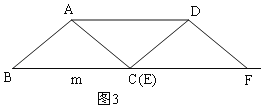
③当AC＝DE时，如图3，此时C与E重合，

m＝8；

综上所述：当m＝或5或8时，△ADE是等腰三角形．

故答案为：或5或8．