题目内容
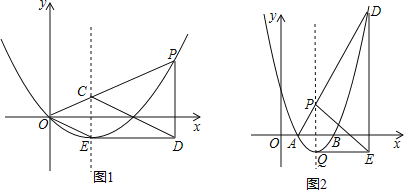
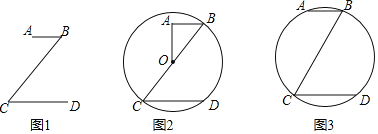
【题目】如图1,有一个“z”字图形,其中AB∥CD,AB:CD:BC=1:2:3.
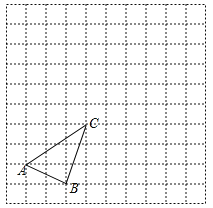
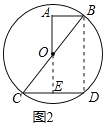
(1)如图2,若以BC为直径的⊙O恰好经过点D,连结AO.
①求cosC.
②当AB=2时,求AO的长.
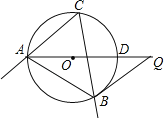
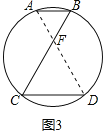
(2)如图3,当A,B,C,D四点恰好在同一个圆上时.求∠C的度数.
【答案】(1)①cosC=![]() ;②当AB=2时,AO=
;②当AB=2时,AO=![]() ;(2)∠C=60°.
;(2)∠C=60°.
【解析】
(1)①连接BD,根据圆周角定理得到∠CDB=90°,根据余弦的定义计算;
②作OE⊥CD于E,证明△AOB≌△EOC,根据全等三角形的性质得到∠A=∠CEO=90°,根据勾股定理计算即可;
(2)证明△AFB为等边三角形,根据等边三角形的性质、圆周角定理计算.
解:(1)①如图2,连接BD,
∵BC为⊙O的直径,
∴∠CDB=90°,
在Rt△BCD中,cosC=![]() =
=![]() ;
;
②如图2,作OE⊥CD于E,
则CE=DE,
∵AB=2,AB:CD:BC=1:2:3,
∴CD=4,BC=6,
∴AB=CE=2,
∵AB∥CD,
∴∠C=∠ABO,
在△AOB和△EOC中,
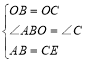 ,
,
∴△AOB≌△EOC(SAS),
∴∠A=∠CEO=90°,
∴OA=![]() =
=![]() ;
;
(2)如图3,连接AD交BC于F,
∵AB∥CD,
∴△AFB∽△DFC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴BF=AB,
∴∠BFA=∠A,
∵AB∥CD,
∴∠B=∠C,
由圆周角定理得,∠A=∠C,
∴∠A=∠B=∠AFB,
∴△AFB为等边三角形,
∴∠C=∠B=60°.

【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?