题目内容
【题目】若抛物线y＝ax2+bx+c（a≠0）与x轴两个交点间的距离为6，称此抛物线为定弦抛物线．已知某定弦抛物线开口向上，对称轴为直线x＝2，且通过（1，y1），（3，y2），（﹣1，y3），（﹣3，y4）四点，则y1，y2，y3，y4中为正数的是（ ）
A. y1B. y2C. y3D. y4
【答案】D
【解析】
根据定弦抛物线的定义结合其对称轴，得到抛物线与x轴的交点坐标，再利用二次函数图象的性质得到结论．
解：∵某定弦抛物线的对称轴为直线x＝2，
∴该定弦抛物线过点（﹣1，0）、（5，0），
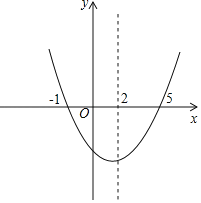
∴该抛物线的大致图象如图所示：
．
所以在（1，y1），（3，y2），（﹣1，y3），（﹣3，y4）四点中，y4为正数．
故选：D．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
