题目内容
2.过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为21,求这个多边形的边数.分析 设这个多边形为n边形,则有n-3条对角线,所分得的三角形个数为n-2,结合该多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为21,即可得出关于n的一元一次方程,解之即可得出结论.
解答 解:设这个多边形为n边形,则有n-3条对角线,所分得的三角形个数为n-2,
∴n-3+n-2=21,
解得:n=13.
答:该多边形的边数有13条.
点评 本题考查了多边形的对角线,熟练掌握“n边形从一个顶点出发可引出(n-3)条对角线,这些对角线分该多边形所得(n-2)个三角形.”是解题的关键.

练习册系列答案
相关题目
10.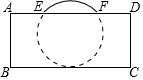 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )| A. | 10$\sqrt{3}$cm | B. | 10cm | C. | 10$\sqrt{2}$cm | D. | 8$\sqrt{3}$cm |
17.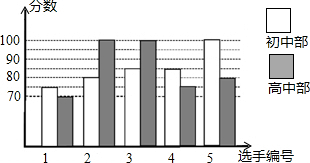 绥棱县第六中学和第一中学联合举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
绥棱县第六中学和第一中学联合举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好?
 绥棱县第六中学和第一中学联合举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
绥棱县第六中学和第一中学联合举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写表;
| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 85 | 100 |
14.下面计算正确的是( )
| A. | 3a-2a=1 | B. | 3a2+2a=5a3 | C. | 3a+3b=6ab | D. | 2x+3x=5x |

 如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE=30°.
如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE=30°.
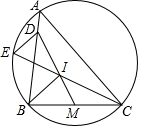 M是BC边的中点,I为内心,连接M、I交AB边于D,连接CI交外接圆于E,证明:$\frac{DE}{EI}$=$\frac{BI}{CI}$.
M是BC边的中点,I为内心,连接M、I交AB边于D,连接CI交外接圆于E,证明:$\frac{DE}{EI}$=$\frac{BI}{CI}$.