题目内容
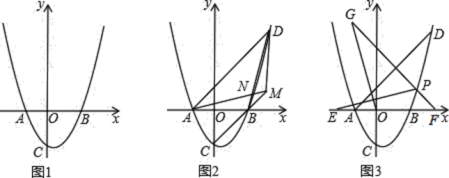
【题目】如图，在平面直角坐标系中，等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系，相似比为1：3，∠ACB＝∠CED＝90°，A、C、E是x轴正半轴上的点，B、D是第一象限的点，BC＝2，则点D的坐标是（ ）
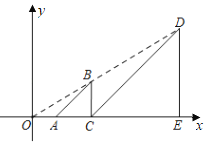
A.（9，6）B.（8，6）C.（6，9）D.（6，8）
【答案】A
【解析】
根据位似变换的定义得到△ACB∽△CED，根据相似三角形的性质求出DE，根据等腰直角三角形的性质求出CE，根据△OCB∽△OED，列出比例式，代入计算即可得到答案．
解：∵等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系，
∴△ACB∽△CED，
∵相似比为1：3，
∴
，即
，
解得，DE＝6，
∵△CED为等腰直角三角形，
∴CE＝DE＝6，
∵BC∥DE，
∴△OCB∽△OED，
∴
，即
，
解得OC＝3，
∴OE＝OC+CE＝3+6＝9，
∴点D的坐标为（9，6），
故选：A．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
