题目内容
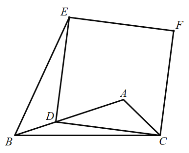
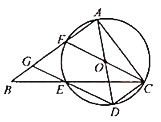
【题目】如图,四边形ABCD中,∠BAC=∠BDC,
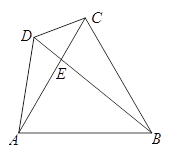
(1)求证:△ADE∽△CEB;
(2)已知△ABC是等边三角形,求证:
① ![]() ;
;
② ![]() .
.
【答案】(1)证明见解析;(2)①证明见解析;②证明见解析
【解析】
(1)证明△BEA∽△DEC,从而得到![]() ,再结合∠AED=∠BEC即可证明△ADE∽△BCE;
,再结合∠AED=∠BEC即可证明△ADE∽△BCE;
(2)①利用等边三角形的性质得到∠ACB=∠BDC,结合∠DBC=∠DBC得到△BEC∽△BCD,根据相似的性质即可得到结果;
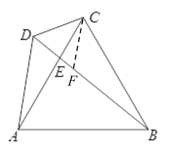
②在DB上取点F,使DF=DC,证明△CDF是等边三角形,再证明△DCA≌△FCB,则有AD=BF,继而得到结论.
解:(1)证明:∵∠BAC=∠BDC,∠BEA =∠DEC
∴△BEA∽△DEC
∴ ![]() ,
,
即 ![]()
又∵∠AED=∠BEC
∴△ADE∽△BCE;
(2)证明:①∵△ABC是等边三角形
∴∠ACB=∠BAC=![]()
∵∠BAC=∠BDC
∴∠ACB=∠BDC=![]()
又∵∠DBC=∠DBC
∴△BEC∽△BCD
∴![]()
∴![]()
②在DB上取点F,使DF=DC
∵∠BDC=∠ACB= ![]()
∴△CDF是等边三角形
∴CD=CF,∠DCF= ![]()
∴∠DCF-∠ACF=∠ACB-∠ACF
∴∠DCA=∠FCB
由△ABC是等边三角形得:AC=BC
∴△DCA≌△FCB
∴AD=BF
∴BD=DF+BF=CD+AD.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目