Question

【题目】如图，AB是⊙O的直径，点C是⊙O上一点（与点A，B不重合），过点C作直线PQ，使得∠ACQ＝∠ABC．

（1）求证：直线PQ是⊙O的切线．

（2）过点A作AD⊥PQ于点D，交⊙O于点E，若⊙O的半径为2，sin∠DAC＝，求图中阴影部分的面积．

Answer 1

【答案】（1）见解析；（2）﹣．

【解析】

（1）连接OC，由直径所对的圆周角为直角，可得∠ACB＝90°；利用等腰三角形的性质及已知条件∠ACQ＝∠ABC，可求得∠OCQ＝90°，按照切线的判定定理可得结论．

（2）由sin∠DAC＝，可得∠DAC＝30°，从而可得∠ACD的 度数，进而判定△AEO为等边三角形，则∠AOE的度数可得；利用S阴影＝S扇形﹣S△AEO，可求得答案．

解：（1）证明：如图，连接OC，

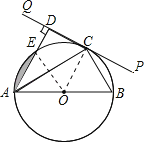
∵AB是⊙O的直径，

∴∠ACB＝90°，

∵OA＝OC，

∴∠CAB＝∠ACO．

∵∠ACQ＝∠ABC，

∴∠CAB+∠ABC＝∠ACO+∠ACQ＝∠OCQ＝90°，即OC⊥PQ，

∴直线PQ是⊙O的切线．

（2）连接OE，

∵sin∠DAC＝，AD⊥PQ，

∴∠DAC＝30°，∠ACD＝∠ABC=60°．

∴∠BAC=30°，

∴∠BAD=∠DAC+∠BAC=60°，

又∵OA＝OE，

∴△AEO为等边三角形，

∴∠AOE＝60°．

∴S阴影＝S扇形﹣S△AEO

＝S扇形﹣OAOEsin60°

＝

＝．

∴图中阴影部分的面积为﹣．