题目内容
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的高,
边上的高,![]() 分别为
分别为![]() 边上的点,将
边上的点,将![]() 分别沿
分别沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 的延长线上点
的延长线上点![]() 处,点
处,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,若
,若![]() ,则
,则![]() 的长是_________.
的长是_________.

【答案】![]()
【解析】
过点D作DH⊥AC于H,由等腰三角形的性质和直角三角形的性质可求∠C=30°,AD= ![]() AC=1,∠DAC=60°,BD=CD,由折叠的性质可得DN=DC,DB=DM,∠CDF=∠NDF,可证△DMN是等边三角形,可得∠MDN=60°,由折叠的性质可求∠HDF=∠HFD=45°,由直角三角形的性质可求解.
AC=1,∠DAC=60°,BD=CD,由折叠的性质可得DN=DC,DB=DM,∠CDF=∠NDF,可证△DMN是等边三角形,可得∠MDN=60°,由折叠的性质可求∠HDF=∠HFD=45°,由直角三角形的性质可求解.
解:如图,过点D作DH⊥AC于H,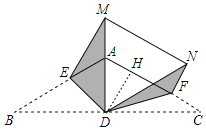
∵AB=AC=2,∠ABC=30°,AD为BC边上的高,
∴∠C=30°,AD=![]() AC=1,∠DAC=60°,BD=CD,
AC=1,∠DAC=60°,BD=CD,
∵MN∥AC,
∴∠DAC=∠DMN=60°,
∵DH⊥AF,
∴∠ADH=30°,
∴AH=![]() AD=
AD=![]() ,DH=
,DH=![]() AH=
AH=![]() ,
,
∵将△ABC分别沿DE、DF折叠,
∴DN=DC,DB=DM,∠CDF=∠NDF,
∴DM=DN,
∴△DMN是等边三角形,
∴∠MDN=60°,
∴∠CDN=30°,
∴∠CDF=15°,
∴∠DFH=∠C+∠CDF=45°,
∵DH⊥AF,
∴∠HDF=∠HFD=45°,
∴DH=HF=![]() ,
,
∴AF=AH+HF=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目