题目内容
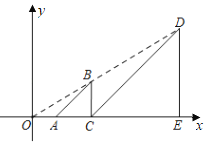
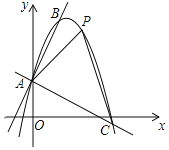
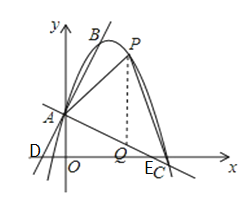
【题目】如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).
(1)求这个二次函数的表达式;
(2)过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.
【答案】(1)y=﹣2x2+4x+1;(2)S△APC最大值为![]() ,此时P(
,此时P(![]() ,
,![]() )
)
【解析】
(1)根据题意设这个二次函数的表达式为y=a(x﹣1)2+3,将A(0,1)代入解方程即可求解;
(2)直线AB与x轴交于点D,直线AC与x轴交于点E,先求得直线AC的解析式,即可求得抛物线和直线AC的交点C的坐标,过P作PQ∥y轴交AC于Q,根据抛物线解析式和直线AC的解析式设出P,Q点坐标,横坐标用t表示,即可表示出PQ,根据S△APC=![]() PQ|xC﹣xA|,得出关于t的二次函数,化为顶点式,即可得到当t为何值时,S△APC有最大值.
PQ|xC﹣xA|,得出关于t的二次函数,化为顶点式,即可得到当t为何值时,S△APC有最大值.
(1)∵抛物线的顶点为B(1,3)
∴设这个二次函数的表达式为y=a(x﹣1)2+3
∵二次函数的图象经过点A(0,1)
∴a(0﹣1)2+3=1
解得:a=﹣2
∴二次函数的表达式为y=-2(x﹣1)2+3,即y=﹣2x2+4x+1
故答案为:y=﹣2x2+4x+1
(2)直线AB与x轴交于点D,直线AC与x轴交于点E,如图所示
∵A(0,1),B(1,3)
设直线AB的解析式为y=kx+b
∴![]()
∴y=2x+1
令2x+1=0
解得x=![]()
∴OD=![]()
![]() ,
,![]()
∵AC⊥AB
∴∠DAE=90°
∴![]()
∴![]()
解得OE=2
∴E(2,0)
设直线AC的解析式为y=mx+n
∵直线AC经过A点,E点
∴![]()
∴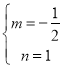
∴直线AC的解析式为y=![]() x+1
x+1
令![]() x+1=﹣2x2+4x+1
x+1=﹣2x2+4x+1
解得:![]() 或
或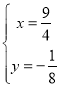
∴C(![]() ,
,![]() )
)
过P作PQ∥y轴交AC于Q
设P(t,﹣2t2+4t+1),则Q(t,![]() t+1)
t+1)
∴PQ=(﹣2t2+4t+1)﹣(![]() t+1)=﹣2t2+
t+1)=﹣2t2+![]() t
t
∴S△APC=![]() PQ|xC﹣xA|=
PQ|xC﹣xA|=![]() (﹣2t2+
(﹣2t2+![]() t)(
t)(![]() ﹣0)=﹣
﹣0)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]()
∴当t=![]() 时,S△APC有最大值
时,S△APC有最大值![]() ,此时,P(
,此时,P(![]() ,
,![]() )
)
故答案为:S△APC最大值为![]() ,此时P(
,此时P(![]() ,
,![]() )
)