题目内容
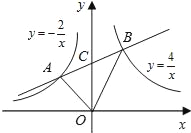
【题目】如图，点A是反比例函数
在第二象限内图象上一点，点B是反比例函
数在第一象限内图象上一点，直线AB与y轴交于点C，且AC=BC，连接OA、OB，求△AOB的面积．
【答案】△AOB的面积是3．
【解析】试题分析：分别过A、B两点作x轴的垂线，构成直角梯形，根据AC=BC，判断OC为直角梯形的中位线，得出OD=OE=a，根据双曲线解析式确定A、B两点的坐标及AD、BE的长，根据S△AOB=S梯形ADBE-S△AOD-S△BOE求解．
试题解析：分别过A、B两点作AD⊥x轴，BE⊥x轴，垂足为D、E，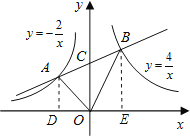
∵AC=CB，
∴OD=OE，
设A（-a，
），则B（a，
），
故S△AOB=S梯形ADBE-S△AOD-S△BOE=
（+）×2a-a×-a×=3．
练习册系列答案
相关题目
【题目】某中学举行演讲比赛，七年级（1）班、（2）班根据初赛成绩各选出5名选手参加复赛，两个班所选出的5名选手的复赛成绩如下面条形统计图所示．
平均分（分） | 中位数（分） | 众数（分） | 方差 | |
（1）班 | 85 | a | 85 | 70 |
（2）班 | 85 | 80 | b | c |
（1）根据条形统计图中的信息，求上表中a，b，c的值；
（2）请你分析说明哪个班级的复赛成绩较好．
