ЬтФПФкШн
ЁОЬтФПЁПФГвНвЉбаОПЫљбаЗЂСЫвЛжжаТвЉЃЌЪдбщвЉаЇЪБЗЂЯжЃК1.5аЁЪБФкЃЌбЊвКжаКЌвЉСПyЃЈЮЂПЫЃЉгыЪБМфxЃЈаЁЪБЃЉЕФЙиЯЕПЩНќЫЦЕигУЖўДЮКЏЪ§yЃНax2+bxБэЪОЃЛ1.5аЁЪБКѓЃЈАќРЈ1.5аЁЪБЃЉЃЌyгыxПЩНќЫЦЕигУЗДБШР§КЏЪ§yЃН![]() ЃЈkЃО0ЃЉБэЪОЃЌВПЗжЪЕбщЪ§ОнШчБэЃК
ЃЈkЃО0ЃЉБэЪОЃЌВПЗжЪЕбщЪ§ОнШчБэЃК
ЪБМфxЃЈаЁЪБЃЉ | 0.2 | 1 | 1.8 | Ё |
КЌвЉСПyЃЈЮЂПЫЃЉ | 7.2 | 20 | 12.5 | Ё |
ЃЈ1ЃЉЧѓaЁЂbМАkЕФжЕЃЛ
ЃЈ2ЃЉЗўвЉКѓМИаЁЪБбЊвКжаЕФКЌвЉСПДяЕНзюДѓжЕЃПзюДѓжЕЮЊЖрЩйЃП
ЃЈ3ЃЉШчЙћУПКСЩ§бЊвКжаКЌвЉСПВЛЩйгк10ЮЂПЫЪБжЮСЦМВВЁгааЇЃЌФЧУДГЩШЫАДЙцЖЈМССПЗўгУИУвЉвЛДЮКѓФмЮЌГжЖрГЄЕФгааЇЪБМфЃЎЃЈ![]() Ёж1.41ЃЌОЋШЗЕН0.1аЁЪБЃЉ
Ёж1.41ЃЌОЋШЗЕН0.1аЁЪБЃЉ
ЁОД№АИЁПЃЈ1ЃЉaЃНЉ20ЃЌbЃН40ЃЌkЃН22.5ЃЛЃЈ2ЃЉЗўвЉКѓ1аЁЪБбЊвКжаЕФКЌвЉСПДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ20ЮЂПЫЃЛЃЈ3ЃЉГЩШЫАДЙцЖЈМССПЗўгУИУвЉвЛДЮКѓФмЮЌГж2.0аЁЪБЕФгааЇЪБМфЃЎ
ЁОНтЮіЁП
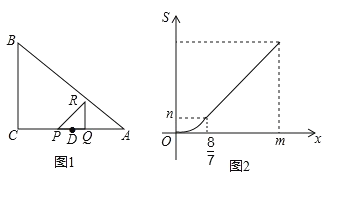
ЃЈ1ЃЉИљОнБэИёаХЯЂДњШыЪ§жЕСаЗНГЬзщЧѓНтМДПЩЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉЕУЕНyЃНЉ20x2+40xЃЌЛЏЮЊЖЅЕуЪНМДПЩЕУЕННсЙћЃЛ
ЃЈ3ЃЉСюy=10ЧѓГіxЕФжЕОЭЪЧЫљЧѓЕФНсЙћЃЛ
ЃЈ1ЃЉЩш1.5аЁЪБФкЃЌбЊвКжаКЌвЉСПyЃЈЮЂПЫЃЉгыЪБМфxЃЈаЁЪБЃЉЕФЙиЯЕЮЊyЃНax2+bxЃЌ
ИљОнБэИёЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃКaЃНЉ20ЃЌbЃН40ЃЌ
1.5аЁЪБКѓЃЈАќРЈ1.5аЁЪБЃЉЃЌyгыxПЩНќЫЦЕигУЗДБШР§КЏЪ§yЃН![]() ЃЈkЃО0ЃЉЃЌИљОнБэИёЕУЃК
ЃЈkЃО0ЃЉЃЌИљОнБэИёЕУЃК
kЃН1.8ЁС12.5ЃН22.5ЃЌ
ЁрaЃНЉ20ЃЌbЃН40ЃЌkЃН22.5ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊyЃНЉ20x2+40xЃЌ
ЁрyЃНЉ20ЃЈxЉ1ЃЉ2+20ЃЌ
ЁрЗўвЉКѓ1аЁЪБбЊвКжаЕФКЌвЉСПДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ20ЮЂПЫЃЛ
ЃЈ3ЃЉЕБyЃН10ЪБЃЌ10ЃНЉ20x2+40xЃЌЛђ10ЃН![]() ЃЌ
ЃЌ
НтЕУЃКxЃН1Љ![]() ЛђxЃН1+
ЛђxЃН1+![]() ЃЈxЃО1.5ЃЌВЛКЯЬтвтЩсШЅЃЉЃЌxЃН2.25ЃЌ
ЃЈxЃО1.5ЃЌВЛКЯЬтвтЩсШЅЃЉЃЌxЃН2.25ЃЌ
ЁрГЩШЫАДЙцЖЈМССПЗўгУИУвЉвЛДЮКѓФмЮЌГж2.25ЉЃЈ1Љ![]() ЃЉЁж2.0аЁЪБЕФгааЇЪБМфЃЎ
ЃЉЁж2.0аЁЪБЕФгааЇЪБМфЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ