Question

【题目】在一次“寻宝”游戏中,已知寻宝图上两标志点A和点B的坐标分别为(-3,0),(5,0),“宝藏”分别埋在C(3,4)和D(-2,3)两点.

(1)请建立平面直角坐标系,并确定“宝藏”的位置;

(2)计算四边形ABCD的面积.

Answer 1

【答案】(1)画图见解析;(2)23.

【解析】试题分析：首先根据点A、B的坐标确定坐标轴的位置，画出图象，再分别过点C、D做x轴的垂线，将四边形ABCD分成△AED，梯形DEFC、△BFC分别求面积再相加即可.

试题解析：(1)以射线AB的方向为x轴正方向.由于线段AB的长为8,将线段AB八等分,找出坐标原点O,于是“宝藏”C和D的位置如图所示.

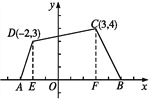
(2)过点C作CF⊥x轴于点F,过点D作DE⊥x轴于点E,则点E,F的坐标分别为(-2,0),(3,0).

S四边形ABCD=S△AED++S△BFC=×1×3+ (3+4)×5+×2×4=23.