题目内容
【题目】问题背景：在△ABC中，AB、BC、AC三边的长分别为
、
、
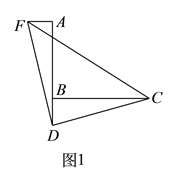
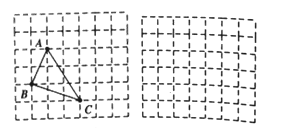
，求这个三角形的面积小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你利用上述方法求出△ABC的面积．
（2）在图2中画△DEF，DE、EF、DF三边的长分别为
、
、
①判断三角形的形状，说明理由．
②求这个三角形的面积．（直接写出答案）
【答案】（1）
；（2）画图见解析；①△DEF是直角三角形，理由见解析；②2
【解析】试题分析：（1）根据题目设置的问题背景，结合图形进行计算即可；
（2）根据勾股定理，找到DE、EF、DF的长分别为
、
、
，由勾股定理的逆定理可判断△DEF是直角三角形．
解：（1）S△ABC=3×3﹣
×1×2﹣
×2×3﹣
×1×3=
；
（2）如图所示：
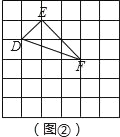
∵DE=
，EF=2
，DF=
，
∴DE2+EF2=DF2，
∴△DEF是直角三角形．
△DEF的面积=
．
练习册系列答案
阅读快车系列答案
相关题目
