题目内容
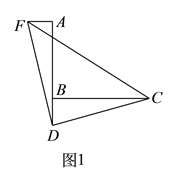
【题目】如图，已知∠BAC＝40°，把△ABC绕着点A顺时针旋转，使得点B与CA的延长线上的点D重合，连接CE.
(1)△ABC旋转了多少度？
(2)连接CE，试判断△AEC的形状．
(3)若∠ACE＝20°，求∠AEC的度数．
【答案】（1）140°；（2）△AEC是等腰三角形；（3）20°.
【解析】试题分析：（1）根据题意求出∠BAD的度数，即旋转角的度数，得到答案；
（2）根据旋转变换的性质得到AC=AE，根据等腰三角形的判定定理判断即可；
（3）根据三角形内角和定理和等腰三角形的性质解答即可．
试题解析：（1）∵∠BAC＝40°，∴∠BAD＝140°，∴△ABC旋转了140°.(3分)
（2）由旋转的性质可知AC＝AE，∴△AEC是等腰三角形．(6分)
（3）由旋转的性质可知，∠CAE=∠BAD=140°，又AC=AE，
∴∠AEC=（180°-140°）÷2=20°．
练习册系列答案
相关题目
