��Ŀ����
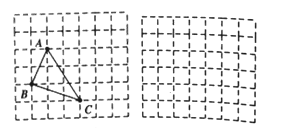
����Ŀ����ͼ��������ABCD�ı�AB�������ϣ������ϵ�A��ʾ����Ϊ��1��������ABCD�����Ϊ16��

��1�������ϵ�B��ʾ����Ϊ�� ����
��2����������ABCD������ˮƽ�ƶ����ƶ���������μ�ΪA��B��C��D�����ƶ����������A��B��C��D����ԭ������ABCD�ص����ֵ����ΪS��
�ٵ�S=4ʱ������ͼ�Σ�����������ϵ�A����ʾ������
����������ABCD���ƶ��ٶ�Ϊÿ��2����λ���ȣ���EΪ�߶�AA�����е㣬��F���߶�BB���ϣ���BF=![]() BB��������t���E��F����ʾ������Ϊ�෴����ֱ��д��t��ֵ��
BB��������t���E��F����ʾ������Ϊ�෴����ֱ��д��t��ֵ��
���𰸡�(1)-5;(2)�ٵ�A'��ʾ����Ϊ��4��2����t=4
�������������������1������������ABCD�����Ϊ16���ɵ�AB�����ٸ���AO=1�������ɵõ�B��ʾ������
��2�����ȸ��������ε����Ϊ16�ɵñ߳�Ϊ4����S=4ʱ�������������������ABCD����ƽ�ƣ�������ABCD����ƽ�ƣ��ֱ���������ϵ�A���ʾ������
�ڵ�������ABCD�����Ḻ�����˶�ʱ����E��F��ʾ������Ϊ�����������ܻ�Ϊ�෴�������������⣻����E��F����ʾ������Ϊ�෴��ʱ��������ABCD�������������˶����ٸ��ݵ�E��F����ʾ������Ϊ�෴�����г����̼������t��ֵ.
�����������1����������ABCD�����Ϊ16��
��AB=4��
�ߵ�A��ʾ����Ϊ��1��
��AO=1��
��BO=5��
�������ϵ�B��ʾ����Ϊ��5��
�ʴ�Ϊ����5��
��2���١������ε����Ϊ16��
��߳�Ϊ4��
��S=4ʱ�������������
��������ABCD����ƽ�ƣ���ͼ1��
A'B=4��4=1��
��AA'=4��1=3��
���A'��ʾ����Ϊ��1��3=��4��
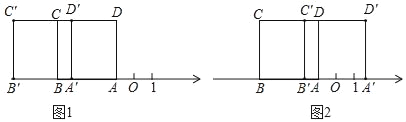
��������ABCD����ƽ�ƣ���ͼ2��
AB'=4��4=1��
��AA'=4��1=3��
���A'��ʾ����Ϊ��1+3=2��
������������A'��ʾ����Ϊ��4��2��
��t��ֵΪ4��
�������£�
��������ABCD�����Ḻ�����˶�ʱ����E��F��ʾ������Ϊ�����������ܻ�Ϊ�෴�������������⣻
����E��F����ʾ������Ϊ�෴��ʱ��������ABCD�������������˶�����ͼ3��
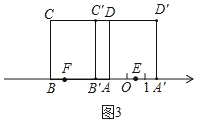
��AE=![]() AA'=
AA'=![]() ��2t=t����A��ʾ��1��
��2t=t����A��ʾ��1��
���E��ʾ����Ϊ��1+t��
��BF=![]() BB��=
BB��=![]() ��2t=
��2t=![]() t����B��ʾ��5��
t����B��ʾ��5��
���F��ʾ����Ϊ��5+![]() t��
t��
�ߵ�E��F����ʾ������Ϊ�෴����
����1+t+����5+![]() t��=0��
t��=0��
���t=4��