题目内容
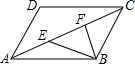
如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,有下列结论:
①S△ADF=2S△BEF;②BF=
DF;③四边形AECD是等腰梯形;④∠AEB=∠ADC.
其中不正确的是______.

①S△ADF=2S△BEF;②BF=
| 1 |
| 2 |
其中不正确的是______.

∵四边形ABCD是平行四边形,
∴BE∥AD,AD=BC,
∴△BFE∽△DFA,
∴
=
,
∵E是BC的中点,
∴BE=
CB=
AD,
∴
=
,
=(
)2=
,
∴①S△ADF=4S△BEF错误;
∴②BF=
DF正确;
∵EC<BC,
∴EC<AD,
∵AD∥EC,
∴四边形AECD是梯形,
∵∠AEC=∠DCE,
∴③四边形AECD是等腰梯形正确;
∵四边形AECD是等腰梯形,
∴∠ADC=∠DAE,
∵AD∥EC,
∴∠AEB=∠DAE,
∴∠AEB=∠ADC,
故④正确.
故答案为:①S△ADF=2S△BEF.
∴BE∥AD,AD=BC,
∴△BFE∽△DFA,
∴
| BE |
| AD |
| BF |
| FD |
∵E是BC的中点,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BF |
| DF |
| 1 |
| 2 |
| S△BEF |
| S△ADF |
| BE |
| AD |
| 1 |
| 4 |
∴①S△ADF=4S△BEF错误;
∴②BF=
| 1 |
| 2 |
∵EC<BC,
∴EC<AD,
∵AD∥EC,
∴四边形AECD是梯形,
∵∠AEC=∠DCE,
∴③四边形AECD是等腰梯形正确;
∵四边形AECD是等腰梯形,
∴∠ADC=∠DAE,
∵AD∥EC,
∴∠AEB=∠DAE,
∴∠AEB=∠ADC,
故④正确.
故答案为:①S△ADF=2S△BEF.

练习册系列答案
相关题目