Question

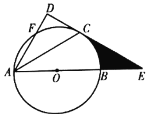
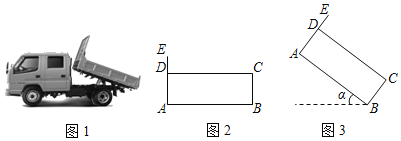
【题目】如图1，是一种自卸货车．如图2是货箱的示意图，货箱是一个底边AB水平的矩形，AB=8米，BC=2米，前端档板高DE=0.5米，底边AB离地面的距离为1.3米．卸货时，货箱底边AB的仰角α=37°(如图3)，求此时档板最高点E离地面的高度．(精确到0.1米，参考值：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)

Answer 1

【答案】点E离地面的高度为8.1米

【解析】

延长DA交水平虚线于F，过E作EH⊥BF于H，根据题意，在Rt△ABF中，求出AF，从而得到EF，结合Rt△EFH，求出EH即可求得结果．

解：如图3所示，延长DA交水平虚线于F，过E作EH⊥BF于H，

∵∠BAF=90°，∠ABF=37°，

∴Rt△ABF中，AF=tan37°×AB≈0.75×8=6(米)，

∴EF=AF+AD+DE=8.5，

∵∠EHF=90°=∠BAF，∠BFA=∠EFH，

∴∠E=37°，

∴Rt△EFH中，EH=cos37°×EF≈0.80×8.5=6.8(米)，

又∵底边AB离地面的距离为1.3米，

∴点E离地面的高度为6.8+1.3=8.1(米)，

故答案为：8.1米．