题目内容
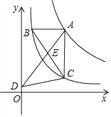
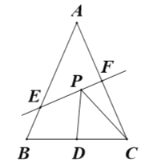
【题目】如图，
的面积为12，
，
，
的垂直平分线
分别交
，边于点
，
，若点
为
边的中点，点
为线段上一动点，则
周长的最小值为( )
A.6B.8C.10D.12
【答案】B
【解析】
先根据中点的定义求出CD，然后可知
的周长=PC＋PD＋CD，其中CD为定长，从而得出PC＋PD最小时，的周长最小，连接AD交EF于点P，根据垂直平分线的性质可得此时PC＋PD=PA＋PD=AD，根据两点之间线段最短可得AD即为PC＋PD的最小值，然后根据三线合一和三角形的面积公式即可求出AD，从而求出结论．
解：∵
，点
为
边的中点
∴CD=
∵的周长=PC＋PD＋CD，其中CD为定长
∴PC＋PD最小时，的周长最小
连接AD交EF于点P，如下图所示
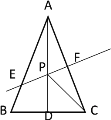
∵EF垂直平分AC
∴PA=PC
∴此时PC＋PD=PA＋PD=AD，根据两点之间线段最短，AD即为PC＋PD的最小值
∵
，点D为BC的中点
∴AD⊥BC
∴
，即
解得：AD=6
∴此时的周长=PC＋PD＋CD= AD＋CD=8
即周长的最小值为8．
故选B．
练习册系列答案
相关题目
