题目内容
【题目】在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示.
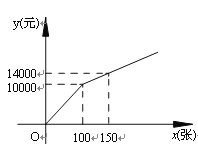
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0≤x≤100时,y与x的函数关系式为 ,当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.
【答案】解:(1) 方案一:y=60x+10000;
当0≤x≤100时,y=100x;
当x>100时,y=80x+2000;
(2)当60x+10000>80x+2000时,即x<400时,选方案二进行购买,
当60x+10000=80x+2000时,即x=400时,两种方案都可以,
当60x+10000<80x+2000时,即x>400时,选方案一进行购买;
(3) 甲、乙单位购买本次足球赛门票分别为500张、200张.
【解析】
(1)根据题意可直接写出用x表示的总费用表达式;
(2)根据方案一与方案二的函数关系式分类讨论;
(3)假设乙单位购买了a张门票,那么甲单位的购买的就是700-a张门票,分别就乙单位按照方案二:①a不超过100;②a超过100两种情况讨论a取值的合理性.从而确定求甲、乙两单位各购买门票数.
解:(1) 方案一:y=60x+10000;
当0≤x≤100时,y=100x;
当x>100时,y=80x+2000;
(2)因为方案一y与x的函数关系式为y=60x+10000,
∵x>100,方案二的y与x的函数关系式为y=80x+2000;
当60x+10000>80x+2000时,即x<400时,选方案二进行购买,
当60x+10000=80x+2000时,即x=400时,两种方案都可以,
当60x+10000<80x+2000时,即x>400时,选方案一进行购买;
(3) 设甲、乙单位购买本次足球赛门票数分别为a张、b张;
∵甲、乙单位分别采用方案一和方案二购买本次足球比赛门票,
∴乙公司购买本次足球赛门票有两种情况:b≤100或b>100.
① b≤100时,乙公司购买本次足球赛门票费为100b,
![]() 解得
解得![]() 不符合题意,舍去;
不符合题意,舍去;
② 当b>100时,乙公司购买本次足球赛门票费为80b+2000,
![]() 解得
解得![]() 符合题意
符合题意
答:甲、乙单位购买本次足球赛门票分别为500张、200张.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】![]() 年
年![]() 月
月![]() 日是我国第六个南京大屠杀难者国家公祭日,某校决定开展铭记历史珍爱和平”主题演讲比赛,其中八(1)班要从甲、乙两名参赛选手中择优推荐一人参加校级决赛,他们预赛阶段的各项得分如下表:
日是我国第六个南京大屠杀难者国家公祭日,某校决定开展铭记历史珍爱和平”主题演讲比赛,其中八(1)班要从甲、乙两名参赛选手中择优推荐一人参加校级决赛,他们预赛阶段的各项得分如下表:
项目 选手 | 演讲内容 | 演讲技巧 | 仪表形象 |
甲 |
|
|
|
乙 |
|
|
|
(1)如果根据三项成绩的平均分确定推荐人选,请通过计算说明甲、乙两人谁会被推荐
(2)如果根据演讲内容、演讲技、巧仪表形象按![]() 的比例确定成绩,请通过计算说明甲、乙两人谁会被推荐,并对另外一位同学提出合理的建议.
的比例确定成绩,请通过计算说明甲、乙两人谁会被推荐,并对另外一位同学提出合理的建议.