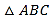题目内容
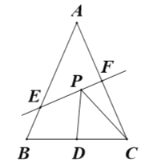
【题目】已知:如图①,![]() 是等边三角形,
是等边三角形,![]() 是
是![]() 边上一点,
边上一点,![]() 平行
平行![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是等边三角形
是等边三角形
(2)连接![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() ,如图②.求证:
,如图②.求证:![]() .
.
【答案】(1)见解析;(2)见解析;
【解析】
(1)根据等边三角形的性质可得∠A=∠B=∠C=60°,然后利用平行线的性质可得∠CDE=∠A=60°,∠CED=∠B=60°,从而得出∠CDE=∠CED=∠C,然后根据等边三角形的判定即可证出结论;
(2)先证出∠DEB =∠DCF,根据等边对等角证出∠DBE=∠DFC,然后利用AAS即可证出△DBE≌△DFC,从而得出BE=CF,然后根据等边三角形的性质和等式的基本性质证出AD=BE,从而证出结论;
证明:(1)∵![]() 是等边三角形
是等边三角形
∴∠A=∠B=∠C=60°
∵DE∥AB
∴∠CDE=∠A=60°,∠CED=∠B=60°
∴∠CDE=∠CED=∠C
∴![]() 是等边三角形.
是等边三角形.
(2)∵∠DEC=∠DCE
∴∠DEB=180°-∠DEC=180°-∠DCE=∠DCF
∵DB=DF
∴∠DBE=∠DFC
在△DBE和△DFC中
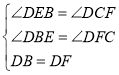
∴△DBE≌△DFC
∴BE=CF
∵![]() 和
和![]() 是等边三角形
是等边三角形
∴AC=BC,DC=EC
∴AC-DC=BC-EC
∴AD=BE
∴![]()

练习册系列答案
相关题目